Assume we want to cross a river with any number of children forming a graph G. How large a boat do we need to be able to make at least a first move?
If the boat leaves the bank, the left bank becomes peaceful. No two vertices left on the left bank can be adjacent in G. Such a subset of the vertex set is called an independent set. The largest size of an independent set in G is denoted by α(G). Therefore, the boat must have at least size n-α(G) in order to be able to make a first move.
A vertex-edge covering of a graph is a subset of the vertex set such that deleting these vertices induces an edgeless graph. The smallest size of a vertex-edge covering in a graph G is denoted by τ(G). In the first moves, all vertices taken on the boat form such a vertex-edge covering. Thus, in order to be able to make a first move, the boat must have size at least τ(G).
 Actually these two concepts are not that different.
If we have an independent set, then the vertices outside this independent set form
a vertex-edge covering. And it also works the other way: The vertices outside of any
vertex-edge covering is an independent set. Therefore we have
τ(G)+α(G) = n for every graph with n vertices.
Actually these two concepts are not that different.
If we have an independent set, then the vertices outside this independent set form
a vertex-edge covering. And it also works the other way: The vertices outside of any
vertex-edge covering is an independent set. Therefore we have
τ(G)+α(G) = n for every graph with n vertices.
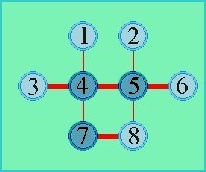
In the example given to the right, the light blue vertices, 1, 2, 3, 6, and 8, form a (largest) independent set, while the dark blue ones, 4, 5, and 7, form a (smallest) vertex-edge covering. But there is another independent sets of size 5, namely 1, 2, 3, 6, and 7, while the vertices 4, 5, and 8 form another vertex-edge covering of this size 3. Thus α(G)=5 and τ(G)=3, and the sum equals 8, the number of vertices.
Therefore, in this example a boat size of 3 is necessary to make the first move. On this page you can check whether you can transfer the graph with a boat size of 3.