Structures like the children in the previous example, together with the conflicts, are called graphs. In a graph we have a set of so-called vertices, like children 1, 2, 3, 4, and 5 in the previous example. But for a set of vertices to form a graph, we must have a certain property that pairs of vertices may or may not have. Pairs of children may be in conflict or not. For other examples, consider the set of all airports, and the property to have a direct flight between the two cities. Or ....
If two vertices have this property mentioned, then we call the pair an edge of the graph, or we call the vertices adjacent. In the left graph below, for instance, vertices 2 and 11 are adjacent, but vertices 7 and 11 are not.
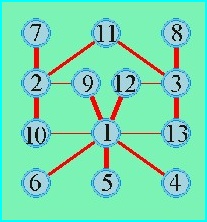
A graph is bipartite if the vertices can be colored by two colors, say black and white, such that no two black vertices are adjacent, and no two white vertices are adjacent. In other words, all edges connect a black and a white vertex in such a bipartite graph. The graph to the right is bipartite, with vertices 1, 3, 5, and 8 colored black and the other vertices colored white.
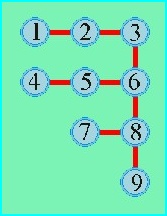
On graphs we can move from vertex to vertex, step by step, along edges. Such movements are called walks. A walk is a sequence x, y, z, ... w of vertices where any two consecutive vertices are adjacent. If no vertex occurs repeatedly in the sequence, it is called a path. If on the other hand the first and the last vertex of the sequence are identical, but otherwise all others are different, then it is called a cycle. For instance, in the graph to the left, 7, 2, 9, 1, 10, 2, 11, 3 is a walk, 2, 9, 1, 12, 3 is a path, and 2, 9, 1, 10, 2 is a cycle.
Finally, a tree is a graph where between every two vertices there is exactly one path. Trees don't have any cycles. The right graph above is a tree. The graph on the previous page is also a tree.