Assume we start with graph G and have a boat of size k.
The state bigraph Bk(G) has all states as vertices.
There is an edge between two states if it is possible to move directly from one to the other.
Obviously, since every move is reversible, we then can move also from the other state to the one state.
The state bigraph is always bipartite, since edges are only possible
between left-boat states and right-boat states.
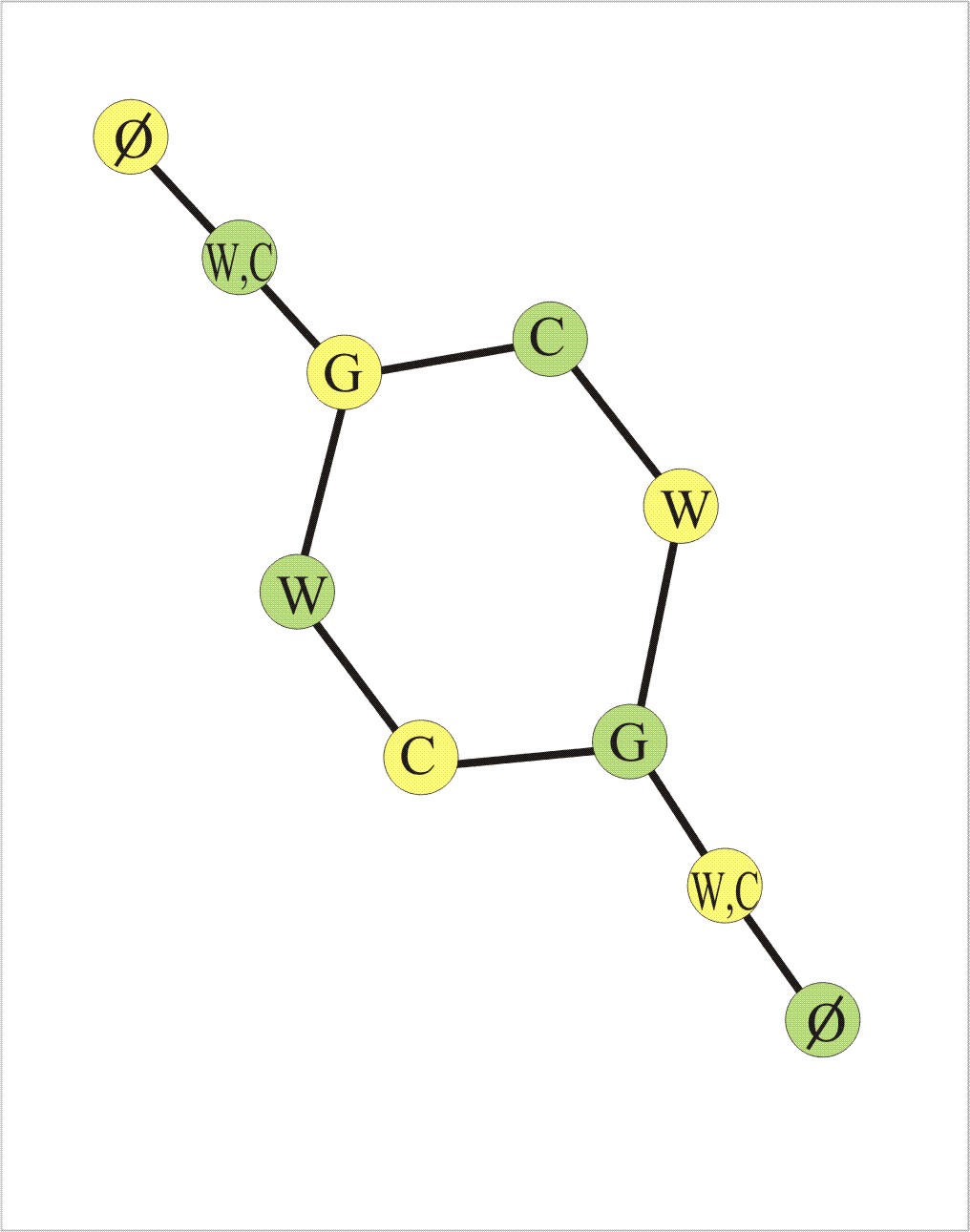
To the right is the state graph of the original Wolf-goat-cabbage puzzle. Left-boat states are yellow vertices, and right-boat states are green vertices. The independent set in the state is listed in the vertex.
Obviously sequences of adjacent states translate into walks in the state bigraph. Therefore the walk yellow-{}, green-{W,C}, yellow-{G}, green-{C}, yellow-{W}, green-{G}, yellow-{W,C}, green-{} is a solution of the puzzle in 7 moves.