Below are several puzzles using the same underlying graph (cage graph). The one on the left and in the middle have the same target state and slightly different initial states. The one on the right has random intial and target states.
| Please solve this. How many moves are needed? | Can you solve this? | Can you solve this? |
The cage graph is bipartite, meaning that the vertices can be colored with two colors, say red and green, such that every edge connects one red and one green vertex. The underlying graph above is bipartite, see the green-red coloring below, whereas the underlying graph of our initial example is not---he triangle can not be colored in this way.
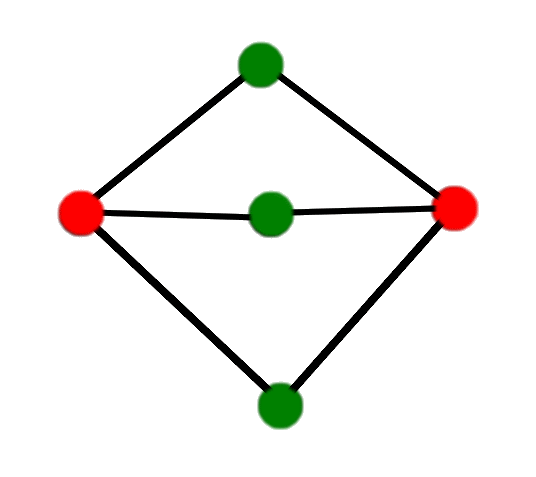
Theorem: The state graph of every bipartite graph is disconnected, and has usually (if the graph has none of the problems discussed before; if it is connected, not a cycle, and has no cut vertex) two connected components of the same size. Thus a puzzle with random intial and target state can be solved in 50% of the cases.
Since the underlying graph of the 15 puzzle is bipartite, it can be solved only for some intial states. The one shown before cannot be solved. That's why it drove everybody nuts.