MAT37x
Franklin College
Spring2004
Erich Prisner,

.

Functions R ---> R²

We have one independent variable, usually denoted, t for time, and f(t) is a vector in two-dimensional space. Thus f(t)=(f₁(t),f₂(t))---we call it the coordinates of a point at time t. We call the equations  x=f₁(t), y=f₂(t) parametric, where  t is the parameter. 

Examples:

Name	Picture	Equations
Astroid		x=a cos3(t) y=a sin3(t) x2/3+y2/3=a2/3
Cardioid		r = 2a(1+sin(Q)) (x2+y2-2ay)2 = 4a2(x2+y2)
Cycloid		x=a(t-sin(t)) y=a(1-cos(t))
Double Folium		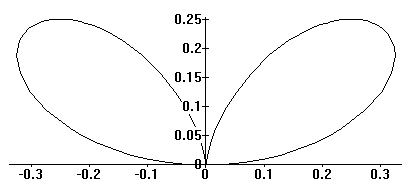r = 4a sin(Q) cos(Q2) (x2+y2)2 = 4ax2y
....		r=cos(2Q) ...

Slope

The slope of the trajectory of the curve is
.
The second derivative is

Arc Length

The length of the trajectory of a curve is given by

Area

The area between the trajectory, x-axis, and the curves x=x(tstart) and x=x(tend) (under the assumption y(t) is positive and x(t) is increasing---otherwise the value expresses what?) is

Polar Coordinates

Sometimes it is more convenient to describe the distance r(t) and angle Q(t) of some point from the origin at time t. These are polar coordinates, instead of the usual cartesian coordiantes  (x(t),y(t)). Obviously the connection between the coordinate systems is  x = r cos(Q), y = r sin(Q) . In a polar curve, r = r(Q) is expressed as a function of Q. In this case

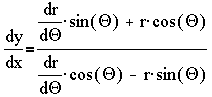
The length of (the trajectory of) a polar curve is .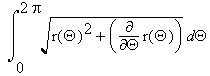
The area inside it equals

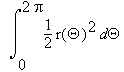
Download a Maple sheet on polar coordiantes.