MAT37x
Franklin College
Spring2004
Erich Prisner,
MAT37x
Franklin College
Spring2004
Erich Prisner,
The cycloid is the curve one sees when looking an a moving bycicle with one part of one wheel illuminated. It is combined by two movements---the circular movement
x=sin(t), y=cos(t)
of the light around the wheel, and the straight movement
x=t, y=1
of the bicycle. The superposition of both movement yields
the parametric equations
x=t-sin(t), y=1-cos(t)
The slope of the trajectory is (dy/dt)/(dx/dt) = sin(t)/(1-cos(t)) .
The length of the trajectory has first been found by Roberval and Wren. It is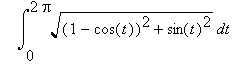 
. The expression under the radical simplifies to
1-2cos(t).
This is ...
Therefore the length of one "bridge" is 8.
The area between the trajectory and the x-axis has independently been found by Torricelli, Fermat and Descartes. It is
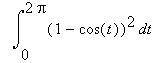. We get a value of
3 P...