The Double Folium

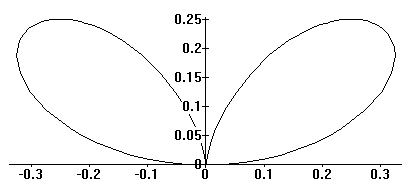In polar coordinates we have r = sin(Q) cos(Q²) In cartesian coordiantes we get (x²+y²)² = 4x²y.

The slope of the trajectory is 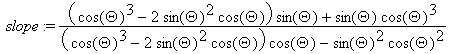. We get horizontal tangents for Q = 0, P/4, -P/4, and vertical tangents for Q = P/6, P/2, 5P/6.

The length of the trajectory is 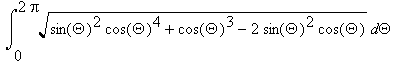, again rather difficult to integrate.

The area enclosed by the trajectory is
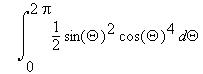
= sin(Q)cos(Q)⁵/12 + sin(Q)cos(Q)³/48 + sin(Q)cos(Q)/32 + Q/32 = P/16 = 0.1963