The Cardioid

One cardioid (that with a=1/2) is easiest defined in polar coordiantes by r = 1+sin(Q). In cartesian coordiantes we would have (x²+y²-y)² = (x²+y²)

The slope of the trajectory is .

For instance, for Q=0, the slope at the point (1,0) is 1.

The length of the trajectory is 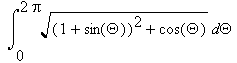, something which is not so easy to integrate (or is it?).

The area enclosed by the trajectory turns out to be 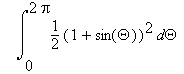, which is equal to
0.75*Q - cos(Q) -cos(Q)sin(Q)/4 = 1.5*P = 4.712