This is a joint section for both the "Graphs" and the "Polyhedra" Chapters. ......
To simplify notation, we define the Euler characteristic c of a polyhedron as c = V-E+F. Thus Euler's conjecture would say that all polyhedra have Euler characteristics equal to 2.
Note that all polyhedra considered so far have this property. What we can and will do first is show that all polyhedra we obtain by dualizing, truncating, glueing, have Euler characteristics 2 provided all polyhedra used in the process have also Euler characteristics 2. We could, for instance, start with the Platonic solids, or with all polyhedra we have found on the previous page.
Therefore many polyhedra have Euler characteristics 2. All platonic solids, all those obtained by glueing two Platonic solids together, all obtained by truncating Platonic solids or thise obtained by glueing so far, all duals of all polyhedra obtained so far, all those obtained by glueing together, or truncatiting, or dualizing any of those obtained so far, and so on.
A graph is plane if it is drawn in such a way that different edges don't meet each other, except at vertices they have in common, of course, where it is unavoidable. Note that edges don't have to be straight lines here, just curves, although with a little effort, by redrawing the location of the vertices, we can draw every plane graph even with straight edges in this way. Below three examples are given:
 |
 |
 |
The edges of any plane graph cut the plane into pieces. These are called the regions or faces of the plane graph. One of them is unbounded, the outer region.
We define the degree of such a region to be the number of edges
bounding it. Surprinsingly twice the edge number does not have to be equal to the sum
of the degrees of all regions, take the graph to the right as an example.
We have three regions, two of degree 4, and the outer one has degree 9.
The sum is 17, but there are 9 edges.
What goes wrong when we try double counting? Well, there may be edges
that are not borders between different regions, but between the same region.
Thus these edges don't contribute twice when counting all bounding edges
of all regions.
Only if we exclude this property, we arrive again at our now familiar property.
So let us call a connected graph 2-edge connected, if
every edge lies between different regions, not like in the example
to the right, where there is an edge separating the outer region from the outer region.
Every 2-edge connected plane graph has a dual, which is also a plane graph, and can be constructed like this. Inside every region of G (including the outer region) we choose one point, the "capital" of that region. Capitals of regions with a common edge are connected by an edge. This edge should only meet the two regions in question---if necessary, we can also draw the edge curved. Click on the "dualize" buttons below the graphs given above for illustrations. Clicking the button again we get the original graph. The dual of the dual is (isomorphic to) the original plane graph.
Since V-E+R didn't change during the steps in (1) and (2), V-E+R=2 also for the initial graph.
This formula is not true for non-connected plane graphs, see the graph to the right,
which has 8 vertices, 8 edges, and 3 faces.
Graphs may be drawn in different ways, some of them plane, some not. Thus we call a graph planar if it allows a plane representation. It turns out that planar graphs cannot have too many edges with relation to the vertex number.
Since the graph K5 of 5 vertices, all of them adjacent to all others, has 10 edges, but could only have 9 if it were planar, is not planar. Problem 1 and 3 above have therefore no solution. Problem 1 asks for a plane representation of K5, which is impossible. If Problem 3 could be solved, the dual of the graph consisting of the parts as regiond would be a plane K5, which is also impossible.
The the graph K3,3 can therefore also not be planar. It has no three mutually adjacent vertices, and 9 edges, but could only have 8 if it were planar. Problem 2 obviously asks for a plane representation of K3,3 which is impossible.
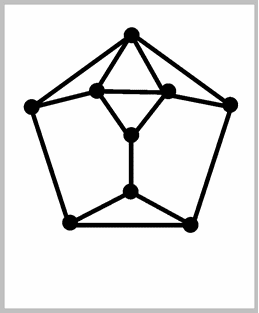
Since polyhedra are 3-dimensional, and as such rather difficult to display, we aim at a good 2-dimensional visualization. Actually, by making all faces transparent, we "see" the graph. Vertices and edges are clearly visible, but not the faces. We would like to "see these faces as well. A good plane projection of a polyhedron is a plane drawing of its graph in such a way that the regions of the graph correspond exactly to the faces of the polyhedron. The "good" should remind us that we require more than just the graph made plane.
The three graphs above are good plane representations of the doghouse polyhedron, of the cube, and of the dodecahedron.
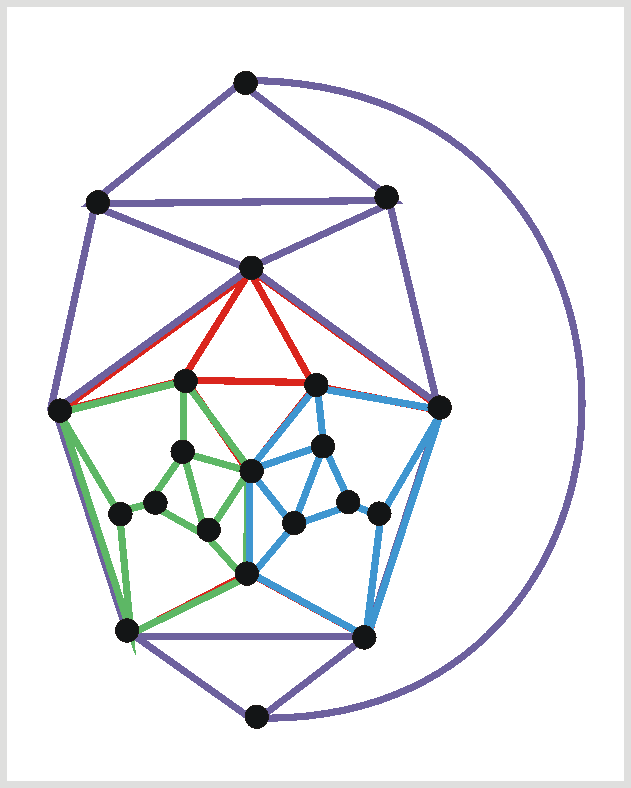
On the other hand, let us check whether the three plane graphs shown below are good plane projections of the polyhedra obtained from two tetrahedra by identifying one vertex, identifying one edge (the red one), and identifying one face (the red triangle).
The first one is not "good". The outer region of the graph does not correspond to a face of the polyhedron, whereas two faces of the polyhedron do not correspond to regions. The second one is not good either: Again the outer region of the graph does not correspond to a face of the "polyhedron" (see the discussion below about whether glueing two tetrahedra along an edge IS a polyhedron), but two faces are not seen as regions. Only the third graph is a good plane projection of the polyhedron. The red glueing face is no longer a face---after glueing it lies inside the polyhedron.
But wouldn't we obtain a good plane projection for any (?) polyhedron in the following way: First we select one of the faces, and make it transparent. Then we place our camera (using a 360° lens!) in the middle of this face. Now we see all faces, vertices, and edges from inside. What we see is a plane graph, and the regions of it are just the faces of the polyhedron.
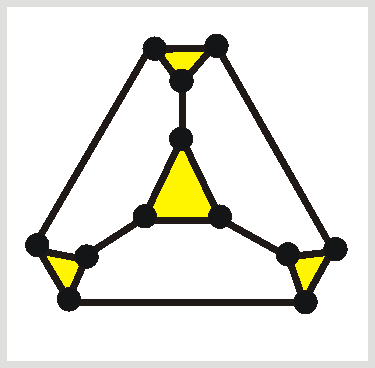
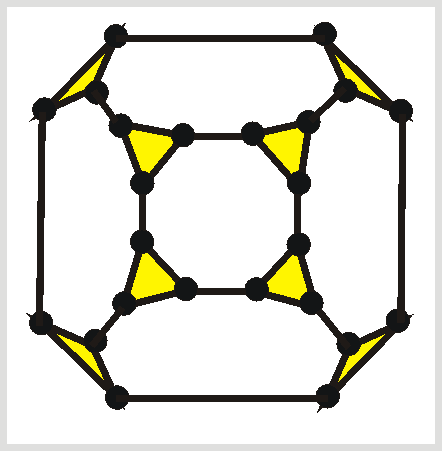
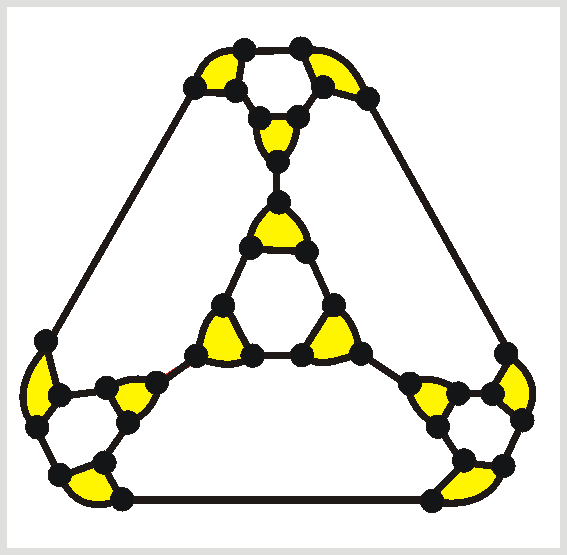
We will continue this discussion below, but let us now move into how to find good plane projections of truncated or glued polyhedra provided we have good plane projections for the original polyhedra. For the truncated polyhedra, we start by a good plane projection of the original polyhedron. Then we draw a small circle around each vertex. We remove all these old vertices, but add new vertices where these circles intersect former edges. These new vertices are connected cyclically by edges, and also attached to the shortened old edges. We get the faces colored yellow below. Below we see projections of the truncated tetrahedron, of the truncated cube, and the truncated truncated tetrahedron.
 |
 |
 |
For the glueing, we start with a good plane projection of the first polyhedron, and a good plane projection of the second one where the face to be glued corresponds to the outer region. These second projection is taken, and put inside the region of the first projection corresponding to the face to be glued in the first polyhedron. Below, to the left, a doghouse projection (in red) is placed inside one face of the dodecahedron. In the other graph, two doghouses (in green and blue) are glued at adjacent 5-gons of another doghouse (in red). Then the resulting polyhedron is glued at another 5-gon of another doghouse.
 |
 |
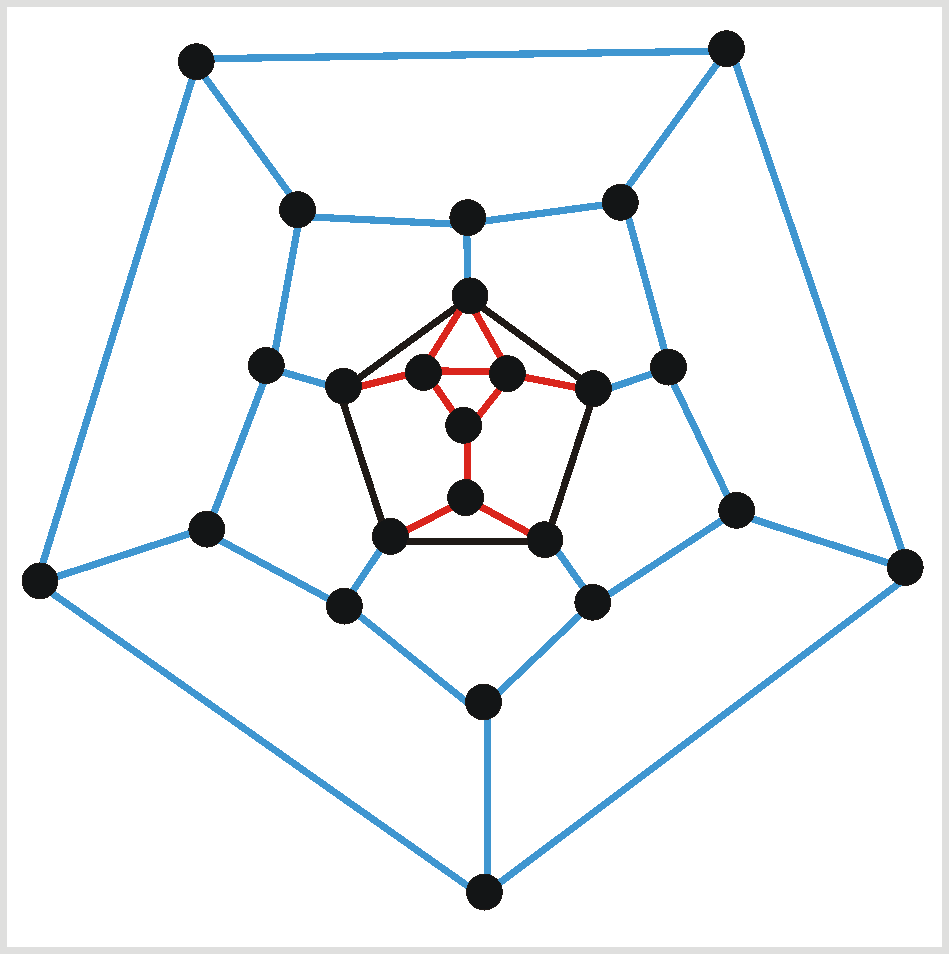The projection of any good plane polyhedron must obviously be connected. Moreover it must even be 2-edge connected.
Next we looked at some polyhedra, that appeared soon after the proof and wouldn't obey the formula.
The Crested
Cube. It has 16 vertices, 24 edges, but only 11 faces (the bottom of the smaller
cube is no face), resluting in V-E+F=3. We discussed what was different to
the polyhedra we have seen before. The ring-shaped face (upper part of the
larger cube) looked suspicious, so maybe we don't allow faces with holes?
We also discussed how this example could be fixed by drawing two diagonals
on the suspicious face, thereby cutting into two normal faces. For this fixed
version, V=16, E=26, F=12, and V-E+F=2 as desired.
The Frame, even when front
and back are divided into two faces each (to obey the "no-holes-in-faces"
condition). We get 16 vertices, 28 edges, and 12 faces, with V-E+F=0 now.
Maybe we shouldn's allow holes in polyhedra?saves the proofs. A body in 3-dimensional space is convex if for every two vertices the whole straight line connecting these points is also insie the body. None of the 5 counterexamples is convex.
A little inprecise, a convex polyhedron can also be described by everything you get from a potato by peeling it with totally straight cuts until no peeling shows.
We discussed why the proof works for convex polyhedra. The first step, the projection can be achieved, since we just go close to any face with a torch to get the desired projection.
Actually it turns out that steps (2) and (3) of the proof always work, all counterexamples don't allow the projection desired in step (1). Therefore we could simply define a Cauchy polyhedron to have no faces with holes, and having the property that removing some face, the polyhedron can be stretched out as described in step (1) of the proof above. Convex polyhedra are special Cauchy polyhedra.
This method of obtaining the proof, and adjusting the definition until it works is in conflict with Euclid's paradigm, which he established in his famous "Elements":
In reality, mathematics rarely worked precisely like this. Definitions (for real number, limits, ...) were rarely specified. As Imre Lakatos claimed, things are more dynamic. It may be worthwhile to save a wrong theorem by changing the definition. Counter-examples drive mathematical progress.
| Draw the plane graph of the following polyhedron: |  |
| Is the following plane graph a good plane projection of a polyhedron? Give some reason for your answer. |  |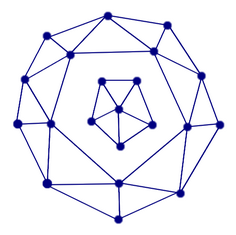
| Is the following plane graph a good plane projection of a polyhedron? Give some reason for your answer. |  |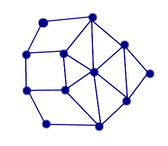
| Find the dual of the following graph. | 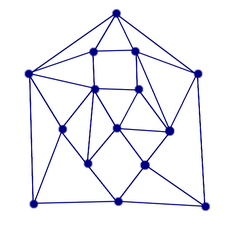 |