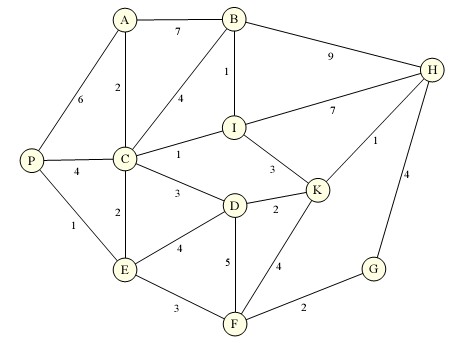

 The streets of a small village are modeled as a graph, like the one shown to the right.
The post car has to drive through all streets every day. Is it possible to find a route that
covers every street (edge) exactly once? This is called an Eulerian Tour.
If the tour starts where it started, it is called closed, otherwise
open. A graph is called Eulerian
if it allows a closed or open Eulerian tour.
The streets of a small village are modeled as a graph, like the one shown to the right.
The post car has to drive through all streets every day. Is it possible to find a route that
covers every street (edge) exactly once? This is called an Eulerian Tour.
If the tour starts where it started, it is called closed, otherwise
open. A graph is called Eulerian
if it allows a closed or open Eulerian tour.
See the famous "house of the Nicolaus" as an example.
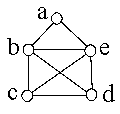
We face two problems:
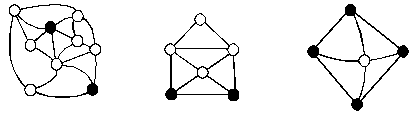
The first problem has to do with the degrees of the vertices. Assume we have an Eulerian tour in a graph. Consider any vertex x that is not the start vertex. At the beginning, all d(x) edges incident with x are untraveled. After having visited x the first time, and having left, two of these edges incident with x have been traveled so far, thus there remain d(x)-2 untraveled edges incident with x. Note that we have to return to x as long as there are untraveled edges incident with x, since we are assuming we are travelling an Eulerian tour. This continues, until eventually we have 1 or 2 untraveled edges incident with x, depending on whether the degree d(x) of x is odd or even. In the first case, as soon as we return to x, we have to stop there. Thus in this case x must be the end vertex of the tour. Thus, if an Eulerian tour is possible, all vertices of odd degree must either be the start or the end vertex of that tour. Therefore, at most 2 of such vertices of degree 2 are possible.
For example, look at the following graphs and test which of them has a Eulerian tour:
Actually we didn't prove the whole theorem yet, just that the condition is necessary. We will show sufficiency of the condition algorithmically, providing an algorithm (called "EULERTOUR") that finds an Eulerian tour if the two conditions are satisfied. This addresses also the second problem mentioned above. We have to describe an algorithm simple enough that every five-year old, when sticking to it, would succeed in finding such a Euler tour. Let's begin with an obvious one, which however, as we will see, will not always be successful.
Therefore, for every graph with at most two verteces of odd degree, every non-Eulerian tour starting on the right vertex (on a vertex of odd degree if that exists) can be extended. Thus eventually we will have found our Eulerian tour.
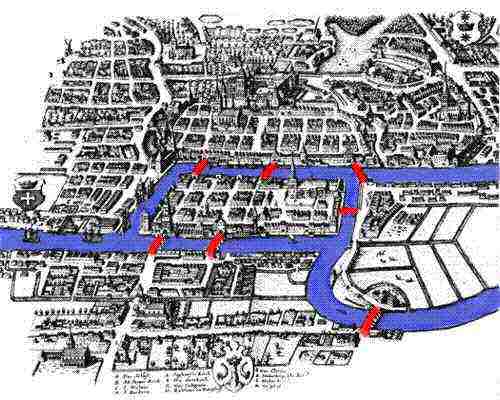 A special case of this problem---whether or not it would be possible to travel through
Königsberg and cross each of the seven bridges exactly once--- was solved by the Swiss
mathematician Leonhard Euler (1707-1783) in 1736. He not only solved the simple special case,
but also provided the general theorem below and started a whole branch of mathematics,
which nowadays is called Graph Theory.
A special case of this problem---whether or not it would be possible to travel through
Königsberg and cross each of the seven bridges exactly once--- was solved by the Swiss
mathematician Leonhard Euler (1707-1783) in 1736. He not only solved the simple special case,
but also provided the general theorem below and started a whole branch of mathematics,
which nowadays is called Graph Theory.
Euler spent his life working in The Russian Academy of Sciences in St Petersburg (1727-1741), and at the Academy in Berlin (1741-1766), and was called back to St Petersburg by Catherine the Great in 1766.