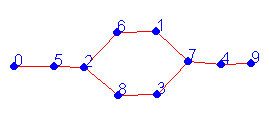
To the right is the state graph of the original Wolf-goat-cabbage puzzle:
Why should we restrict ourselves to induced subgraphs of this grid red box graph? This graph is bipartite, but maybe nonbipartite graphs give us something more interesting? Why shouldn't there be three students who mutually hate each other? In the setup phase, click on the word "next graph" on the bottom of the applet to get different red boxes. Adjacent students still will fight, but also students having the same letter, or containing some common letter. Click twice until you see "Graph 2" in fromt of it. There are two students with letter F. You can also not leave them on the same bank alone.
Difficulty Level 3: Try the following example: Click twice on "next graph" until you get "Graph 2" as described. Choose students "B", "E", "J", "R", and both "F"s. Click on "Start". You can transfer them to the right bank in 9 moves.
Difficulty Level 4: Try also this example: Choose "Graph 1" by clicking on "next graph". Choose students "HO", "F", "J", "K", "M", "E" (in the fourth row), "O", "P", and "R". Now you cannot leave "HO" and "O" on one side, they would fight as well. Adjust your boat size to 3 by clicking on "increase size?". Click on "Start". You can transfer them to the right bank in 9 moves.
There is another graph relevant to this game. The state graph has all states as vertices. There is an edge between two states if it is poosible to move directly from one to the other. Obviously, since every move is reversible, we then can move also from the other state to the one state. Note that the state graph is always bipartite, since edges are only possible between boat-left states and boat-right states. Note also that, by the definition of states, every vertex of the state graph must be in an edge. The state graph does not contain so-called isolated vertices.
Question 5: Given the encodings of two states, when are they adjacent (again with boat size k)?
To the right is the state graph of the original Wolf-goat-cabbage puzzle:
Below is the state graph for the (difficulty 3) example you tried above: The game graph is given to the right.
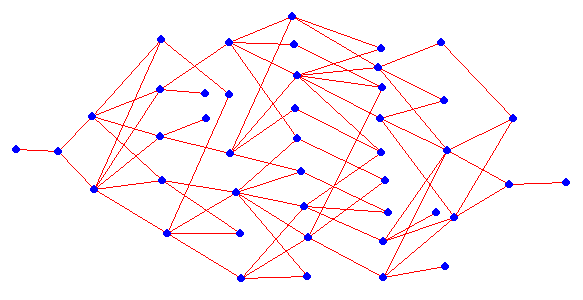
Research Question: Are there game graphs where we can solve the puzzle (i.e. move all our students from left to right), but where the state graph is not connected (i.e. some state distribution of students to left and right can not be achieved from our start of all students on the left bank)?
In general, the state graph may be disconnected.
Given a graph and a fixed vertex x, how do we compute these levels? Well, in the first level we collect all neighbors of x (which is the only vertex in level 0). In the second level we collect all of the remaining vertices which are adjacent to some vertex in the first level. And so on. By the construction, each vertex has a neighbor in the level one below, and all edges are either inside some level or between consecutive levels.
From this drawing of the state graph, it is possible to draw several interesting conclusions. For instance, how likely is it that a monkey, making its moves completely randomly, solves the problem in the minimum number (9) of moves? Well the answer is about 1/4686. Using the very simple rule to never reverse a move immediately, the probability increases to 1/533. Do you want to know why?
Erich Prisner, 2002-2004