Erich Prisner

Probabilities for shortest paths

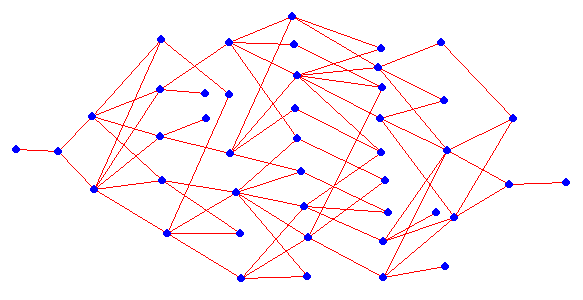
Given is the graph below. Starting on the leftmost vertex x, a bug moves randomly on it. How likely is it that it reaches the rightmost vertex y in the minimum number (7) of moves?

Note that the levels of a given distance to x are ordered in columns separated by the green lines.

if there is some shortest (length 7) path from the leftmost vertex x to the rightmost vertex y using that particular vertex.

How do we detect which vertex to color red? We detect the red vertices in level 7, then in level 6, then in level 5, and so on. In level 7, y is red. In level 6, a vertex is red if it has a red neighbor in level 7. In level i, a vertex is red if it has a red neighbor in level i+1.

Now we compute for each red vertex z the probability p(z) that the bug arrives there in the minimum number of steps. We compute these numbers from lower levels to higher levels. In level 0, the probability that we arrive after 0 steps at x is 1. If all probabilities for red vertices in all levels lower than k have been computed, how do we compute the probability for a red vertex z in level k? Let v1, ... vt be the red neighbors of z in level k-1. How could the bug end on z after k moves? It must either

Thus p(z) = p(v1)/d(v1) + p(v2)/d(v2) + ... + p(vt)/d(vt). We get a probability of about 1 : 494.

What if we use the additional rule that we never immediately reverse a move? Since then the monkey will never return to where it came, all transfer probabilities (except in the first move) rise to 1/(d(v1)-1). We get a probability of about 1 : 29.

Now, what is the probability that the bug goes from y to x in 7 steps? Of course, we could redraw the graph (the levels are different now) and analyze the question using the same tool. If you are interested in questions like this, go to the page on random walks, which may also be used to answer the question.

Given is this graph (see here for information on the context).

We
The probability for success for the bug is 1/4686.
Without reversing moves we get 1/533.

Let's do another example (see here for the context). The probability we get is 1/15,116,544
Without reversing moves we get 1/6912.


Erich Prisner 2002-2004