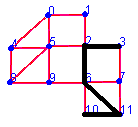
In how many steps can you shunt the 4-car train in the middle into the position to the left? (Click on the first or last car to define it to be the head of the train. This head is then marked by a red line. Then get moving by clicking near the middle of the rail the head will go in the next step. Reverse by clicking on the last car.)


Here is another one. It's possible to do it in 10 steps.
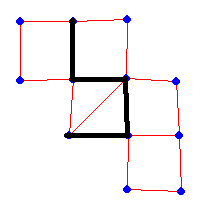

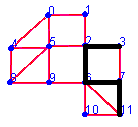
Here is another a harder nut. Do it in 18 steps. Can you see that there is some train configurations that you cannot move at all?
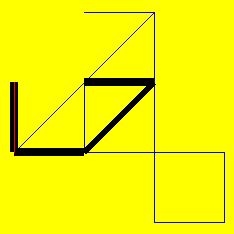

Do you still have problems doing it? Well, the problem is tough! How likely is it that a monkey (clicking randomly) does it in the minimum number of moves? The probability (assuming that the monkey transforms each configuration into any configuration obtainable form that with the same likelihood) for that is lower than for having all six numbers right in lotto, it is 1/15116544. Even when the monkey avoids going back to the same configuration immediately, the probability is 1/6912. See here why that is so.
Here is another one. Do it in 9 steps. Can you see that there are two train configurations that you cannot move at all?

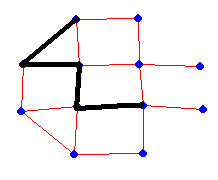
Here is another one. Do it in 10 steps.