Functions R ---> R³

We have one independent variable, usually denoted, t for time, and f(t) is a vector in three-dimensional space. Thus f(t)=(f₁(t),f₂(t),f₃(t))---we call it the coordinates of a point at time t. We call the equations x=f₁(t), y=f₂(t), z=f₃(t) parametric, where t is the parameter.

Examples:

Name

Picture

Equations

Astroid

x=a cos³(t)
y=a sin³(t)

x^2/3+y^2/3=a^2/3

Cardioid

r = 2a(1+sin(Q))

(x²+y²-2ay)² = 4a²(x²+y²)

Double Folium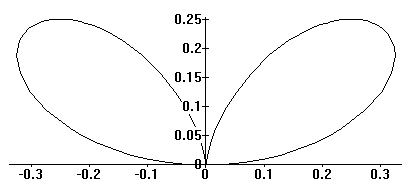

r = 4a sin(Q) cos(Q²)

(x²+y²)² = 4ax²y

Velocity, Acceleration

The velocity of the point is the derivative of f, i,e, the function f'(t) = (f₁'(t),f₂'(t),f₃'(t)). The speed is the absolute value of the velocity. The acceleration is the second derivative f''(t) = (f₁''(t),f₂''(t),f₃''(t)) of f.

Let T=f'(t)/|f'(t)| denote the unit tangent vector for time t .

.

Functions R ---> R³

Examples:

Velocity, Acceleration

Arc Length and Curvature

Cylinder Coordinates

Spherical Coordinates

.

Functions R ---> R3

Examples:

Velocity, Acceleration

Arc Length and Curvature

Cylinder Coordinates

Spherical Coordinates

Functions R ---> R³