Theory Chapter 3:
Sequential Games I:
Perfect Information and no Randomness

In the chapter we look at another class of rather simple games, namely sequential games. These are games where the players move one after another, no two players move at the same time. Among sequential games we concentrate on games of perfect information, where every player knows all previous decisions when he or she moves. Randomness will also only be included after the next chapter. We will learn a little terminology, see how to display these games either as game tree or game digraph, and how to analyze them using the tool of "backward induction" provided the game is finite. We conclude the chapter by discussing whether this solution found by backward induction would really always be what real players would play, by discussing another approach for sequential games and discussing the special roles two-person zero-sum games play here, and also by discussing briefly several existing sequential games like chess, checkers, tic-tac-toe. We also mention a rather simple approach how one would play if not knowing how to play.

• 1. Extensive Form: Game Tree and Game Digraph
• 2. Analyzing the Game: Backward Induction
  • Finite Games
  • The Procedure
  • Zermelo's Theorem
  • Historical Remark: Ernst Zermelo
• 3. Additional Topics
  • 3.1. Reality Check and Utilities
  • Modeling Note 3: Modeling Altruism using Utilities
  • 3.2. Playing it Safely---Guaranteed Payoff
  • 3.3. Two-player Zero-sum Games
  • Historical Remark: John von Neumann
  • 3.4. Breaking Ties
  • 3.6. Existing Games
  • 3.7. Greedy Strategies
• References
• Exercises and Projects

A sequential game, is a game where the players move one after another; never are two players supposed to move at the same time. Remember that a position is usually any situation where a player has to make a move, a decision, out of a number of possible moves. Therefore in a sequential game such a position is linked to just one of the players. Later, when we allow randomness, positions may also be situations where a random experiment is performed, so later positions may also belong to the random player. In addition to these positions belonging to some player, there are also positions where the game ends, these are called end positions. They are the outcomes, and obviously nobody is supposed to move then anymore. But at these end positions, the payoff for each player must be given. Every game starts with one and only one start position.

Note that the relevant information known to the player about to move is also part of the position. Usually in a sequential game of perfect information this information is just the sequence of all previous decisions of the other players in all previous moves. If this differs, we usually also have different positions, except in cases where this difference is not relevant for the future. We will explain this more thoroughly below when we explain the difference between Game Trees and general Game Digraphs.

In this chapter we assume perfect information and don't allow random moves. Perfect information means in the context of sequential games that every player will immediately recognize in which position the game presently is.

The game changes its position by moves of players. At each non-end position, the player linked to that position chooses one of his or her possible moves. These possible moves are also known to everybody. Each of these possible moves of the player to move leads to another position.

Sequential games are usually visualized or even described graphically: For each position a small circle is drawn on the paper, and the possible transitions between the positions are expressed by an arrow between the corresponding circles. Very often, instead of arrows one uses straight lines or even curves, from left to right or from up to down, with the convention that the direction is leftwards (in the first case) or downwards (in the second). We usually use lines from left to right. The small circles are usually denoted as vertices or nodes, and the arrows are denoted as arcs. These vertices and arcs are usually labeled. At each non-end vertex, there is a label indicating to whom the vertex belongs, The outgoing arcs of a non-end position correspond to the possible moves the player can make at this position. They are labeled by the move names. The end positions are those vertices with now outgoing arcs---at them the payoffs for each player have to be noted. The whole (directed) graph with all labels is called the Game Digraph or Extensive Form of the sequential game. But note that we need to extend the definition further later, when we take randomness and non-perfect information into account.

In the SENATE RACE II example above, the Extensive Form looks as follows.

Let us look at another example:

The Extensive Form for the NIM(6) game described above, looks as follows. If, following chess terminology, the first mover is called "White" and the other one "Black", then White's positions, moves, and payoffs are colored red, and Black's positions, moves, and payoffs blue. Every position has a label indicating how many stones are still on the desk at that position, and who's move it is. For instance, "4w" is the position with four stones on the desk and White to move.

The Extensive Forms in the previous two examples are so-called Game Trees. Let's avoid the formal definition and just say that a Game Tree looks like a tree, rotated by 90 or 180 degrees. Trees arise if one considers a position to be the whole sequence of previous decisions made by all the players who have moved so far.

But in the previous example, it is also obvious that there is some redundancy. Why do we have two "3w" positions? Granted, both have a different history, one resulting from position "5b" with Black taking two stones, and the other from position "4b" with Black taking one stone. But that is not relevant for the future, as can be seen in the Game Tree by the fact that both subtrees hanging at the corresponding vertices are identical. So if White decides how to play in these two positions, he or she should come to the same conclusion.

If we identify such corresponding positions in the Game Tree of the previous Nim(6) example, we get the following Extensive Form:

It should have become clear from the previous discussion that games may have different descriptions by Extensive Forms. We will see more examples later. Note also that in the literature mostly game trees are used to describe extensive forms. Our approach of game digraphs has the advantage of reducing the number of positions.

Next we will discuss a simple and very powerful method how to analyze sequential games. However, this method works only for so-called "finite games". A sequential game is finite if it has a game tree with finitely many vertices. Having a Game Digraph> with finitely many vertices is not sufficient, as can be seen in the next example:

How do you play this simple zero-sum game? Who will win? Obviously nobody will lose, since losing can very easily be avoided. So if nobody loses, nobody wins. The two players will continue playing forever. The Game Tree goes on and on, indicated by the dashed line, and is therefore infinite. Thus the game is not finite.

We can also use a Game Digraph. Then a non-end position is uniquely determined by who is about to move, White or Black, and how many fingers were last shown. So we have four of these positions, labeled as W1, W2, B1, and B2. Of course there is one more position, the start position with White to move, where no fingers have been shown yet, and two end positions, one where White wins and one where Black wins.

Why does the previous example have a finite game digraph although the game is not finite? The reason is that the game digraph is cyclic. That means that it is possible to follow arcs from some vertex x and reach the vertex x again after some time, like in W1, B2, W1 in the above example. Games with a cyclic game digraph have always an infinite game tree, but a sequential game is finite if it has some acyclic (not cyclic) finite game digraph. Why does the previous example have a finite Game Digraph although the game is not finite? The reason is that the Game Digraph has cycles. It is possible to follow arcs from some vertex x and reach the vertex x again after some time, like in W1, B2, W1 in the above example. Thus a sequential game is finite if it has some acyclic finite Game Digraph.

There are theoretical reasons why we exclude these infinite games, but of course there are more practical reasons: We need to have a guarantee that a game eventually ends. Note that even chess would not be finite, were it not for the "50-move rule" that says that a chess play ends as draw if no pawn has been moved within 50 moves.

What players may want from Game Theory is advice how to play. In a sequential game that means that for every position that is not an end position the player who has to move there would need advice about which of his or her possible options to choose. Such a list of recommendations for all the player's positions---even for those positions for which we are rather certain that they will never occur in a play--- is called a pure strategy for that player. In this section we will present a procedure generating pure strategies for all players. Moreover, at each vertex some numbers will be attached by the procedure: the likely payoffs for each one of the players. The word "likely" has nothing to do with probabilities, which will only be discussed in the next chapter. Its meaning here will be discussed later.

Let us explain the method first at another example, this time a non-zero sum game with three players:

The Game Tree of this game is shown to the right. The behavior of legislator C is easiest to explain first, since at the time when C has to move, A and B have already moved. So C doesn't need to anticipate their strategies. C may face four different situations, corresponding to the four vertices to the right of the tree. In the first situation, when A and B have already voted for a raise, C can keep face by voting against the raise but still get the benefit of it. The same is true if A and B both rejected the idea of a raise and it is decided already. It is different if one voted for and one against a raise. Then C's vote counts. Since the money is more important than face (for our fictitious legislators only!) C would vote for a raise in that case.

Now everybody can do this analysis, therefore if B has to decide, she can anticipate C's reactions. If A voted for a raise, B knows that C will vote for a raise if she votes against, and conversely. So why not give C the burden of having to vote for the raise? Obviously B will vote against a raise in this situation. If on the other hand A voted for a raise, then B has to vote for a raise to keep things open.

Since A knows all this too, A will vote against a raise, B will vote for it, and C will vote for it as well. A has the best role in this game. Going first is sometimes useful, after all!

This method of attaching a recommendation and "likely" payoffs for all players to all vertices of the Extensive Form, starting at the vertices "late" in the game and moving backwards is called "backward induction". We will explain it more formally below.

Note that when a player accepts these decision found by backward induction, he or she must assume that the other players will also stick to these backward induction recommendations. And why wouldn't they? Well, one reason could be that they are not able to analyze the game, since the game is maybe too complicated. Or a player can analyze the game, but doubts that all others can do so.

There is still one problem in this procedure. What do we have if there are ties, if two or more successor vertices of a vertex have the same likely payoff for the player to move at that vertex. This case will be discussed in Section 3.4

In 1913, Ernst Zermelo showed that finite perfect-information sequential games can always be analyzed using backward induction. Actually he referred to chess, but this result can easily be generalized to the following:

By construction, the outcome generated by backward induction obeys the following property, which of course has some conncetion to the Nash equilibrium definition:

Although the backward induction solution seems to be the best the players can do in many situations, there are certain sequential games where players tend to play differently:

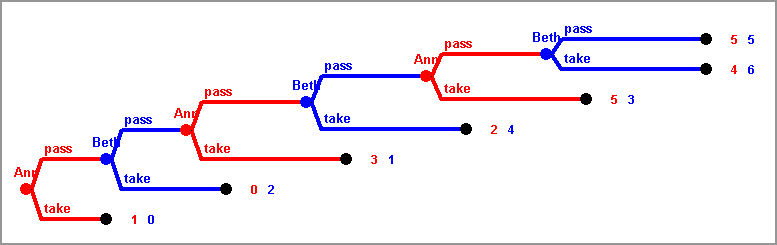
This game was introduced by Rosenthal [Rosenthal 1981] in the 100 rounds version. It has a unique backward induction solution: Player 1 would take the money in the first round and end the game. On the other hand, players can both increase their payoff if they both wait much longer. When McKelvey and T. Palfrey made experiments with this game [McKelvey, T. Palfrey 1992], they observed that players tend to play some rounds before somebody cannot resist any longer and takes the higher stack.

Here is another classical example:

The graph to the left shows the extensive form of the game when payoffs mean the money obtained. In the backward induction solution Ann would offer only one bill, or maybe even none---we will discuss this problem with payoff ties in a later subsection---to Beth. However, experiments show that people tend to be less mean than they could. People like to be fair.

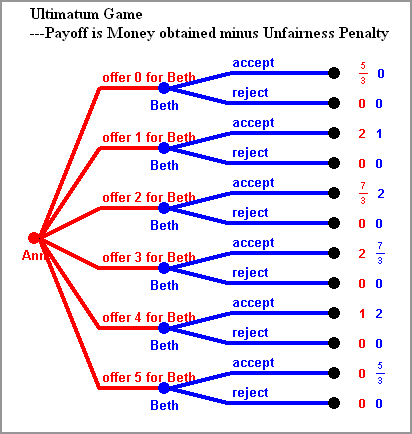
Let us try to model dissatisfaction of unfairness in the following way: Let the payoff of each player not be just the money obtained, but rather express satisfaction about the outcome. Assume this satisfaction is the money obtained, but reduced by an "unfairness penalty" for the player obtaining more. Assume this unfairness penalty is two thirds of the difference between both values. That means that the money exceeding the amount the other gets is still valuable, but only one third of this surplus money satisfies. Then the payoffs of this modified Ultimatum Game can be seen in the figure to the right. The backward induction solution is Ann offering two bills to Beth, which she accepts.

A player will only get the payoff predicted by backward induction analysis if all players play rationally, i.e. stick to the backward induction analysis moves themselves. Thus this "likely" payoff is not guaranteed: if the other players deviate from backward induction moves, a player may get much less. Therefore using these backward induction moves may be risky. If you want to play it safe, maybe assuming that all others do intend to just hurt you, like in the Maximin paradigm discussed in the previous chapter, you may want to play different moves. See the next example:

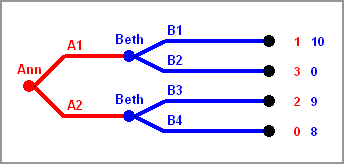In this game Ann owns one position, the start position, and there are two positions where Beth is supposed to move, and there are four end positions.
The backward induction analysis goes as follows: In Beth's first position, Beth will choose move B1, and in her second position Beth will choose move B3. Therefore the likely payoffs at these two positions are 1, 10 respectively 2,9. Therefore Ann will choose move A2, since this will give her a payoff of 2.
However, if Ann doubts Beth's rationality, if maybe Ann fears that with Beth's payoffs of 9 and 8 in the end positions following Beth's second position Beth may chose any one of B3 and B4, then maybe Ann will move A1, since this can guarantee her at least a payoff of 1.

Sequential games with perfect information have guaranteed payoffs, also called security levels, for all players. These can be found for every player separately, doing a variant of backward induction, which will be called Security Level Analysis. Let's call the player in question Ann. During this analysis we also find what moves Ann would choose in each of her positions if she would fear that everybody is just playing to hurt her. The resulting strategy is called her Security Strategy. Since this is a completely egocentric point of view, taking only the payoffs for Ann into account, we can eliminate all other payoffs for this analysis. Then we attach a value, the guaranteed payoff for Ann, to every position, starting again at the end positions. For moves with all successors having already guaranteed payoffs for Ann attached, we choose the lowest of these values as the value for the position provided Ann does not move at that position, and the largest of these values of the successors provided Ann does move at that position. In that case Ann will choose the option leading to a position with maximal guaranteed payoff for Ann attached.

Consider the following game. There are 11 non-end positions, named as Pos1, ... Pos11.

• indicates a likely payoff of 10 for Ann and of 6 for Beth.
• shows that Ann can only guarantee a payoff of 5. To guarantee that payoff, Ann would choose move A2 in position Pos1, instead of A1 in the backward induction strategy. In position Pos6 she will also act differently. Since only Ann's payoffs are relevant for this analysis, only they are highlighted in yellow.
• Finally shows that Beth has a security level of 3. Again, Beth would sometimes, as in position Pos3, move differently than in the backward induction strategy. Here only Beth's payoffs are highlighted.

This fact gives tremendous significance to backward induction in the two-player zero-sum case. Therefore it seems justified to call the two backward induction strategies of the two players "optimal". If both players, Ann and Beth, stick to these strategies, they will obtain the values attached at the start position as payoffs. If one of them, let's say Beth, deviates, we already know that Beth will get not more. This is even true without the assumption of two-players zero-sum games. But with this additional assumption, if Beth deviates we also know that Ann will not get less, provided Ann sticks to her backward induction strategy.

What happens in the backward induction procedure above if in step (P3) there are two or more successor vertices, let's say "W" and "U", giving both the maximum value for player X to move? Player X would be totally indifferent whether to move to W or to U. The value for X at V is obviously the value for X at W (which is the same as the value for X at U), but still the decision where to move would influence the payoffs of the other players. The most natural solution to these problems is to assume that X will move to W or U with equal probability. This is already a so-called "behavior strategy"---at certain vertices a player would not be determined what to play but rather alternate two or more moves in a random way. Then we call X a "neutral" player. Obviously the value for any other players at V would be computed as the average (expected value with 50-50 probabilities) of the values for that player at W and U.

In a two-person game, a slightly different approach could also be taken. If player X is slightly "hostile" against her opponent, she would choose that vertex of W and U that has the lower value for her opponent. If X is slightly "friendly" she would choose that vertex of W and U that has the higher value for her opponent. Note that she still cares only about her payoffs, only in a tie situation of her own payoff she would consider the other's payoff. Hostile players can be modeled by subtracting a small fraction (let's say 0.1%) of her opponent's payoffs from her payoffs, a fraction so small that the ordering of the payoffs is not changed, only in case of ties suddenly the situations are ordered. Similarly, a friendly player would add a small fraction of the opponent's payoffs to her own payoffs.

Friendly players are far from being altruistic. However, altruistic behavior can also be modeled using the same trick, but for real altruism one would add a considerable amount of the opponent's payoff to the player's own payoff.

There are even more ways of breaking ties, also for more than one player. A player may be friendly to some players and hostile to others. Backward induction analysis must be changed in each of these cases.

Board games are, almost by definition, games of perfect information, since everything is in the open provided no cards are part of the game. They are also very often sequential games, where the players take turns to move. Well-known example of board games are Chess, Go, Nine Men's Morris, Checkers, Pachisi, Backgammon with a very long history, or the more recent games of Monopoly, Hex, Tic-tac-toe or others. Some, like Pachisi, Backgammon, and Monopoly, are played with dice or even with cards that are revealed, and contain therefore randomness. But Chess, Go, Checkers, Tic-tac-toe, Hex are all two-players zero-sum finite sequential games without randomness and with perfect information. So shouldn't people play the backward-induction strategy? The simple and quick answer is: Yes, they should, but in some cases backward induction analysis has just not yet been performed. Thus the backward induction strategy, the optimal strategy, is unknown in many cases.

Tic-tac-toe is the simplest of these games, with the smallest game tree. The game tree has just 5478 positions. The game has been analyzed, and the expected outcome is a draw. You can play tic-tac-toe here against the computer.

Checkers will always result in a draw when played correctly ([von Nievergelt and Gasser 1994].

On the other hand, for Chess and Go the number of possible positions is so large that even with the help of the most advanced computers a full analysis is not expected for soon. Chess has about 10⁴³ positions, a number with about 43 digits, and Go even about 2·10¹⁷⁰. Checkers has about 10¹⁸ positions and Nine Men's Morris about 10¹⁰ positions.

How do chess computers play? We have already seen that the complete extensive form is not available---it is simply too large. Therefore backward induction is also not an option. These existing chess programs usually have two ingredients: Starting at a position, they look a few moves ahead, instead of looking back. Secondly a chess program, the same as an experienced chess player, has values attached, or can attach values, to every possible position. They are supposed to be approximations of the likely payoffs found by backward induction, but they are not obtained by looking any further to successors of the position considered. Rather features of the position are considered and expressed into a value using a more or less complicated formula. In chess, material advantage are part of these features to consider, but there are also finer features, like the number of possible moves of a position, or pawn structure, and so on.

Very often such evaluations of positions come very naturally. For instance, for many games the evaluations might be the payoff if the game just ended there.

Now a Greedy strategy decides what to do in a position by simply looking at all possible successor positions, and choosing the one where the evaluation for the player to move is highest. More generally, a k-Greedy strategy looks just k moves ahead, and chooses the Maximin or backward induction choice of this small part of the Game Digraph.

What's next?

• Uri Zwick, Micahel S. Paterson, The Memory Game, Theoretical Computer Science 110 (1993) 169-196.
• E. Zermelo, Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels, Proceedings of the Fifth International Congress of Mathematicians 2 (1913) 501-504.
• Reisch, Diploma Thesis
• R. Rosenthal, Games of Perfect Information, Predatory Pricing, and the Chain Store, Journal of Economic Theory 25 (1981) 92-100.
• R. McKelvey, T. Palfrey, An experimental study of the centipede game, Econometrica 60 (1992) 803-836.
• Steven M. LaValle, Planning Algorithms, Cambridge University Press 2006.