Exercises for Chapter 3: Sequential Games I: Perfect Information and no Randomness

1. Draw the extensive form of the following game:
   TWO-ROUND BARGAINING(5,3): Five dollar bills are to be shared by two players. Ann makes an offer how to share them, which Beth can either accept or reject. If she accepts, the bills are divided as agreed upon. If the rejects, two dollar bills are taken away and only three remain on the desk. Then Beth makes an offer how to share these three dollars, which Ann can accept or reject. If Ann accepts, the bills are divided accordingly, if she rejects, nobody gets anything.
   Draw the extensive form of the game, and perform backward induction analysis. Remember that you don't have to use a Game Tree---you can also use a digraph to simplify matters.
2. Analyze the following game:
   MATCHING CHAIRS: Ann and Beth can select both 3 chairs out of 7 totally available chairs, two L-chairs and five O-chairs. One L-chair is worth $300, but if you have a pair of L-chairs, the pair is worth even $800. O-chairs are less valuable: One is worth $100, a pair is worth $400, but three of them are worth $900. Beginning with Ann, Ann and Beth alternate selecting a chair until each of them has three.
   Draw the extensive form of the game, and perform backward induction analysis.
3. Analyze the 3·3 version of REC THE SQUARE game. Draw the extensive form of the game, and perform backward induction analysis. Note that you can describe the game using the following 18 states, where each symbol subsumes the cases obtained by rotation and reflection. State 0 is the Start, and states 12, 16, and 17 are the terminal states. 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17:
4. Analyze the 3·3 version of CREATING HOLES, a variant of REC THE SQUARE. Draw the extensive form of the game, and perform backward induction analysis. Note that you can describe the game using the following 18 states, where each symbol subsumes the cases obtained by rotation and reflection. State 0 is the Start, and states 12, 16, and 17 are the terminal states. 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17:
5. Analyze the game TAKE SOME(8,60%,10), described here. Draw the extensive form of the game, and perform backward induction analysis.
6. Analyze the game TAKE SOME(12,60%,10), described here. Draw the extensive form of the game, and perform backward induction analysis.
7. Find the backward induction solution and perform security level analyssis of the following game:
8. Find the backward induction solution and perform security level analyssis of the following game:
9. Find the backward induction solution and perform security level analyssis of the following game:
10. Find the backward induction solution and perform security level analyssis of the following game:
11. Find the backward induction solution and perform security level analysis of the following game:
12. Find the backward induction solution and perform security level analysis of the following game:
13. Find the backward induction solution and perform security level analysis of the following game:
14. Find the backward induction solution and perform security level analysis of the following game:
15. Find the backward induction solution and perform security level analysis of the following game:
16. .....
17. Find the backward induction solution and perform security level analysis of the following game:
18. Find the backward induction solution and perform security level analysis of the following game:
19. Draw the extensive form of the following sequential game. Try to draw a game digraph, not a game tree.
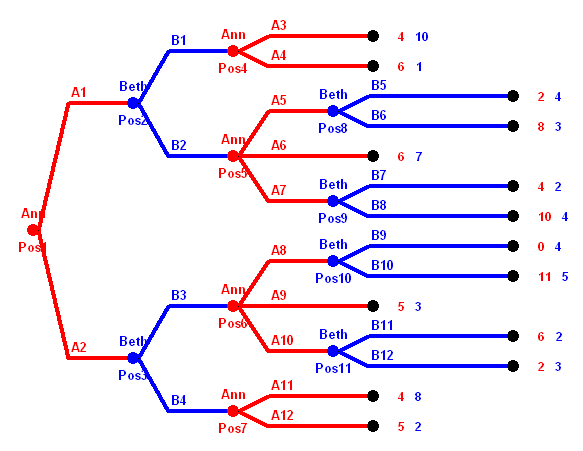
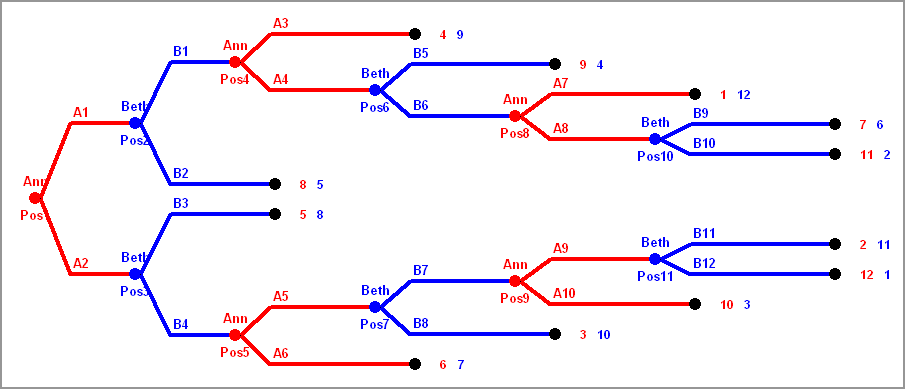
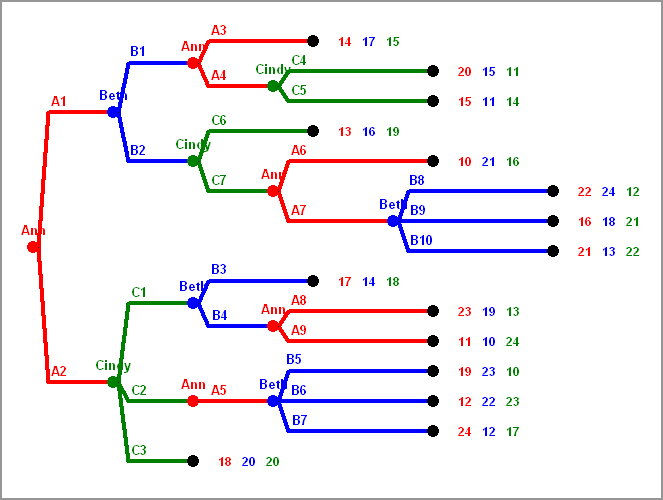
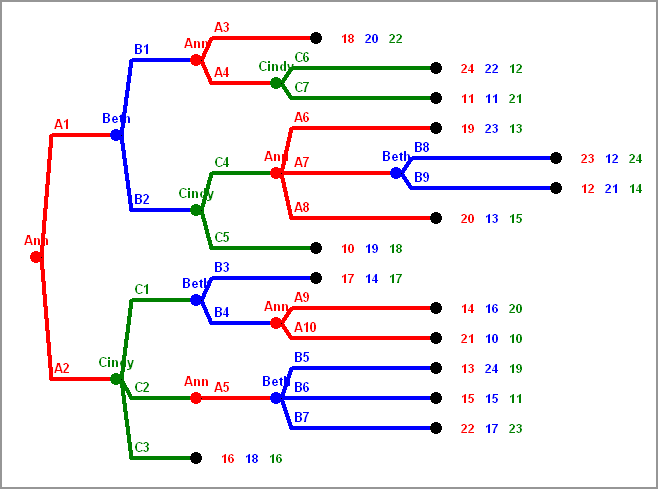
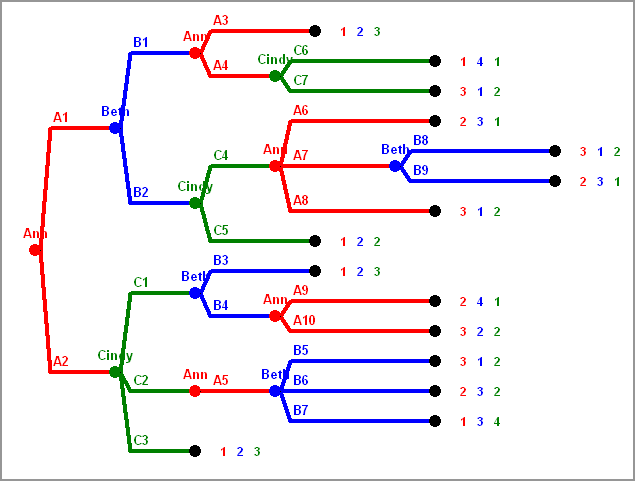
    There are three players, A, B, C. At the beginning A has a dollar note. In each round the player having the dollar note has to give it to one of the other two players. After 5 rounds, after the dollar note has moved 5 times, the game is over and the player having it can keep it.
20. Draw the extensive form of the following sequential game. Try to draw a game digraph, not a game tree.
    There are three players, A, B, C. At the beginning B and C have one dollar note each. In each round the player without dollar note can grab the dollar note from one of the other two players. After 6 rounds the game is over and the player having a dollar note can keep it.
21. Draw the extensive form of the following sequential game. Try to draw a game digraph, not a game tree.
    There are four players, A, B, C, and D, sitting in a cyclic order. At the beginning A has a dollar note. In each round the player having the dollar note has to give it to the player to the right, or to the player sitting opposite, but not to the player sitting to the left. After 6 rounds, after the dollar note has moved 6 times, the game is over and the player having it can keep it.
22. Draw the extensive form of the following sequential game. Here you have to use the Game Tree.
    CHOCOLATES In THE BOX (5): There are four players, A, B, C, and D, sitting in a cyclic order. At the beginning A holds a box containing 5 pieces of chocolate. In each round the player having the box eats one (just one!) of the pieces of chocolate and then has to give the box to the player to the right, or to the player sitting opposite, but not to the player sitting to the left. After 5 rounds, the chocolate is gone. The payoff for each player is the number of pieces of chocolate he or she has eaten.
23. Draw the extensive form of the following sequential game. Here you have to use the Game Tree.
    CHOCOLATES In THE BOX (6): There are four players, A, B, C, and D, sitting in a cyclic order. At the beginning A holds a box containing 6 pieces of chocolate. In each round the player having the box eats one (just one!) of the pieces of chocolate and then has to give the box to the player to the right, or to the player sitting opposite, but not to the player sitting to the left. After 6 rounds, the chocolate is gone. The payoff for each player is the number of pieces of chocolate he or she has eaten.
24. 5 PIRATES with hierarchy, tie means yes: Five pirates with a strict hierarchy have to decide decide how to distribute 20 gold coins they have found. They do it according to the following rules. In each round the highest ranking pirate (left) has to propose a distribution of the coins. This proposal is voted on, with the proposer voting too, and even deciding in case of a tie. That implies that in case of only two pirates, the proposal will always win, and in case of four pirates, the proposer needs only one of the others voting for the proposal. If the proposal wins, everything is settled. If not, the proposer is thrown into the water and dies, and the next round starts. Assume that the pirates value their life worth 40 gold coins, and prefer throwing somebody overboard if everything else is equal (are playing the "hostile" variant).
    What would you propose if the bottle points on you and there are 2, 3, 4, or 5 pirates left?
25. 5 PIRATES with hierarchy, tie means no: Five pirates with a strict hierarchy have to decide decide how to distribute 20 gold coins they have found. They do it according to the following rules. In each round the highest ranking pirate (left) has to propose a distribution of the coins. This proposal is voted on, with the proposer voting too. Different to the version in the previous exercise, in case of a tie the proposal is rejected. If the proposal wins, everything is settled. If not, the proposer is thrown into the water and dies, and the next round starts. Assume that the pirates value their life worth 40 gold coins, and prefer throwing somebody overboard if everything else is equal (are playing the "hostile" variant).
    What would you propose if the bottle points on you and there are 2, 3, 4, or 5 pirates left?

1. Project: TAKE SOME: Analyze the game TAKE SOME(n,p%,q), described here., in the most general form, with all parameters open. Draw the extensive form of the game, and explain what will happen if both play optimal, depending on the parameters.
2. Project: SHUBIK AUCTION(A,B,n):
   Two players, Adam and Bob, bid sequentially for an item. worth A units for Ann and B units for Beth. The bids must increase in increments of 10. Adam starts by either bidding 10 or by passing (in which case, Beth gets the item for nothing). If Adam bids 10, Beth can bid 20 or pass, and so on. After one player passes, the other player gets the item for her highest bid, but different to ordinary auctions, the other player still has to pay her highest bid but gets nothing in return. There is a fixed maximum number n of rounds.
   Explain what happens for different parameters A, B, and n. For example you could start with

   • A=25, B=35, n=10,
   • A=50, B=35, n=9,
   • A=15, B=25, n=9.

   and then explain what happens in general.
   This project is extendable later, if you want to continue with it.
3. Project: WHO's NEXT(n) Three players play a sequential game with n moves. At each move, the player who has to move decides which one of the other two players has to move next. Ann starts in move 1. In move n, the player to move decides which one of the other two players wins a payoff of 1. The two players that don't win get a payoff of 0.
   Since this is a sequential game with a lot of payoff-ties, the question is how small sympathies and antipathies between the players would affect the outcome. What happens if A likes B and C, but B hates A and likes C, and C likes A and hates B, for instance. There are obviously many cases to consider.