Prerequisites: Chapters 1, 2, and 4.
Imagine you are playing poker and the organizer of the tournament approaches your desk, tips you on the shoulder, and tells you not to pass that often. Would you be amused? In a liberal society, we are used that organizations and governments leave us as much freedom as possible. Of course, there are always rules. Pay your taxes, don't speed, don't smoke during class, but we want these rules to be minimum, and we enjoy the freedom of selecting our own moves. But in many cases, players' behavior can be influenced in a more subtle way by those in charge. All they need to do is to change the rules. Increase the taxes for flying and the people will more often drive by car or train. But the government insists that you still have your choice. Only that the unwanted choice is no longer rational and optimal.
In 1994, the FIFA, the World Soccer Association, changed the rules for assigning points in soccer tournaments. Before that, a win counted as 2 points, a draw 1 point, and a defeat as 0 points. With the new rule, a win is even 3 points worth. Expressed aim was to encourage teams to play more offensive again, after years of rather defensive, unattractive play. In this Chapter we will discuss a game---not soccer but still a game with defense, midfield and attack--- where changing the point system will influence how coaches set up their teams.
This game is played on a field divided into three subfields called "left", "midfield" and "right". Two teams, A and B, play against each other. Each team sends 5 players on the field, where each player goes into a subfield and stays there during the whole game (later this requirement is weakened and we allow some movements between fields). At the beginning, and after each "goal", the referee throws the ball into the midfield. One player in the midfield will catch the ball---we always assume that if the ball is thrown into a subfield, then one player there catches it.
A ball may never been thrown directly from left to right field, or from right to left field.
Starting the ball in the middle part, the time until the ball returns to the middle part or a goal is shot is denoted as round.
How should the players play? What is the best strategy for a team? Of course, the coach should select players that can catch and throw the ball well, that are alert, fit, and have a good eye. But what exactly does this mean? And should different types of players be selected? Even more difficult is to tell how the individual players should play, where they should stand, how they should move, and where to throw the ball. We are not trying to find advice for this highly complex game. Rather we only consider the question of how the coach should distribute the players into the three parts, assuming that all players are more or less equal. Therefore we neglect all these many moves of both teams, and rather model it as a simultaneous game between the two coaches, each coach having only one move---choosing the distribution. Note that you are not allowed to react to the distribution of your opponent's team. You have to announce your distribution before the game, without knowing the other team's distribution.
Think about it for a moment. which distribution do you think is best, which distribution would you choose as a coach?
If you want to simulate the game without the sweat, try this applet.
Each distribution of the five A-players is described by three numbers: DA (for defense) is the number of A-players in the left field, MA (for midfield) is the number of A-players in the midfield, and AA (for attack) is the number of A-players in the right field. Of course DA+MA+AA=5. In the same way, DB, MB, and AB are numbers of B-players in the right, middle, and left field, and again DB+MB+AB=5. Because of this condition of adding up to 5, each such distribution can even be encoded by a pairs of numbers, (DA,MA) for the A-player, and (DB,MB) for the B-player. There are 21 such pairs of numbers with sum at most 5.
If team A uses distribution (DA,MA) and team B uses distribution (DB,MB),
how likely is a goal for A and how likely is a goal for B in a round?
Recall that a round is defined by two steps:
the ball moving out of the midfield, and then moving to the goal or back to the midfield.
We make the basic assumption that all players are equal; if a ball is thrown into
a subfield, each of the players there has an equal probability of catching it.
Then the probability that the goal initially goes to the left field is
MB/(MA+MB). If this happens, the probability of a B-player catching the ball in the left field,
and therefore for a goal for B is AB/(AB+DA), where AB=5-DB-MB, and AA=5-DA-MA.
See the probability tree to the right.
The probability for a goal for B is
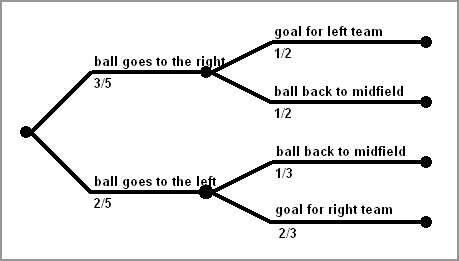
Let us compute pA and pB for distribution (1,3) against distribution (1,2). We get pA = 3/(3+2)·1/(1+1) = 3/5·1/2 = 0.3, and pB = 2/(2+3)·2/(2+1) = 2/5·2/3 = 4/15 = 0.267. The probability tree in this case is shown to the right.
Computing the expected value of goals for Team A in one round is quite simple. We have a value of 1 with probability pA and a value of 0 with probability 1-pA, therefore the expected value equals pA·1 + (1-pA)·0 = pA. In the same way, pB is the expected value of goals for Team B in the round, and the expected goal difference is pA-pB.
The goal of soccer is to score goals and avoid getting goals.
Thus the goal difference might be considered as the payoff we want to maximize, although
we will see in Section 4 that this approach is not quite accurate.
It is straightforward to compute the expected values of the goal difference in
one round for different player distributions, as has been
done in this Excel sheet on the sheet "matrix".
If the payoff is the goal difference, then we have a zero-sum simultaneous game,
where the payoffs are computed by random experiments based on the choices of the teams.
The best response digraph, actually the condensed version used for symmetric games,
is displayed to the right. Recall that when an arrow goes from vertex (1,1) to vertex (0,3),
then (0,3) is Ann's best response to Beth's move (1,1), but (0,3) is also Beth's best
response to Ann's move (1,1).
The 21 moves for each player are ordered in an obvious grid where the
three corners of the resulting triangular structure correspond to distributions with
strong attack, strong midfield, and strong defence, and where the relation of each
other distribution to these three corners indicates its emphasis on defence,
midfield, or attack, respectively.
From this digraph there follows that this matrix has four pure Nash equilibria, the first one (1,3) versus (1,3), the second one (2,2) versus (2,2), and the third and fourth one (1,3) versus (2,2) and (2,2) versus (1,3).
Not too surprising for a 21×21 matrix, it doesn't have any strong domination but weak domination. Note that (2,2), which is part of a pure Nash equilibrium, is still weakly dominated by (1,3). After deleting all weakly dominated moves, the moves (0,1), (0,2), (0,3), (0,4), (1,1), (1,2), and (1,3) remain for both players. In this 7*7 matrix, the moves (0,1), (0,2), and (1,1) are weakly dominated. After deleting these as well, the resulting 4*4 matrix has a weakly dominating move (1,3). Therefore the IEWD equilibrium of this one-round consideration would be the move (1,3).
There are two maximin moves for both players: The moves (1,3) and (2,2). The maximin analysis is done on the Excel sheet mentioned above on the "matrix" sheet. In column Z the minima of the row values are computed, and the maximum of these values, the Maximin value, is in cell Z9. For Beth, in row 31 the maxima of the column values are computed. Since this is a zero-sum game so far, the payoffs of Beth's are the opposites of Ann's payoffs, therefore the minima of Beth's values are the maxima of the corresponding Ann's values. The minimum of these maxima values can be found in cell D31. In both cases, the red values show where these maxima or minima are attained.
It is maybe not surprising that the midfield seems to be important, but why are attack and defence not symmetric? The move (1,2), which is the symmetric counterpart to (2,2), occurs in none of these concepts as recommendation for a move.
We move our emphasis back from games to experiments.
In particular, we are again assuming in this section that both player distributions
are already fixed. However, now we look at a 3-round experiment consisting of three
rounds of the basic experiment discussed above. The outcome is a result of the game, like 1:1 or 1:2 or 1:0,
for example. Since no more than 3 goals can be achieved in 3 rounds,
there are 10 possible outcomes, as shown in the Probability Digraph to the right.
There are three kinds of arcs, those of probability pA which are colored green,
those of probability pB which are colored red, and those of probability p0
that are colored black. Remember that pA, pB, p0 are
the probabilities for a goal of team A,
for a goal of team B, and for no goal in any round.
Formulas for pA, pB, p0 have been derived in Section 1.
Let us compute the probabilities for reaching each of the outcomes above. As discussed before, we want to assign probabilities to all situations in the Probability Digraph. Let us abbreviate the situation with a standing of a:b after n rounds by a:b|n, and let p(a:b|n) denote the probability with which it will occur. The beginning situation 0:0|0 has probability 1. The three situations 1:0|1, 0:0|1, and 0:1|1 occur with probabilities pA, p0, and pB. More interesting are the six situations after two rounds.
These probabilities could also be derived in a more elegant combinatorial way.
Since the first four outcomes mean win for A, the next two draw, and the last four a win for B, the probabilities for each of these events can be expressed as well by rather complicated formulas. For instance, A wins with probability pA3 + 3·pA2·p0 + 3·pA2·pB + 3·pA·p02. The probability for a draw is 6·pA·pB·p0 + p03. The probability for a loss for Ann is 3·pB·p02 + 3·pA·pB2 + 3·pB2·p0 + pB3.
As in Section 1 we could ask about the expected numbers of goals for A and B, but now for the 3-rounds experiment. But this question is rather easy to answer. Remember that if you repeat an experiment n times, the expected sum of the random variable in these n experiments equals n times the expected value of the random variable in a single experiment. Therefore the expected number of goals for A in the 3-round experiment is 3·pA, and the expected number of goals for B equals 3·pB. The expected goal difference of the 3-round experiment equals 3·(pA-pB).
But the payoff for a soccer match are not the number of goals, or the difference between the goals your team scored and the opponents goals. Rather the payoff are points you get for win, draw, and loss. Usually you get 3 points for a win, 1 for a draw, and no point for a loss. Therefore soccer is not a zero-sum game! Therefore the expected value of points for Ann equals
Let us again turn the focus from probability experiments, where we cannot act but just observe, towards games. The formulas for the expected number of points derived in the previous section have to be evaluated for all possible values of DA, MA versus all possible values of DB and MB. This is obviously again a task best left for Excel. On the file DMA2.xls on the sheet "3-round analysis", the expected number of points are computed. In the black cells you can change the number of points assigned for win and draw. The Best responses are computed on the sheet "BestR".
Using this file, let us compare three different rules. The old 2-1 rule, assigning 2 points for a win and 1 point for a draw, the new 3-1 rule, assigning 3 points for a win and 1 point for a draw, and also a 3-2 rule. It turns out that the differences in the best response digraph are small. The best response digraph for the 2-1 rule looks exactly like for the goal difference considered above. The two other best response digraphs are shown below.
Let me describe the differences. Going from the 2-1 to the 3-1 rule, the best response to (0,3) is no longer (1,3) but (0,4), (2,2) is no longer a best response to (1,3), and (1,3) and (2,2) are no longer best responses to (2,2). Going from the 2-1 to the 3-2 rule, (1,3) is no longer a best response to (1,3), and (1,2) and (1,3) are no longer best responses to (2,2). Under the 3-1 rule, the distribution (2,2) loses some of its attractivity, and the only pure Nash equilibrium is (1,3) versus (1,3). Under the 3-2 rule, the only pure Nash equilibrium is (2,2) versus (2,2).
Thus in our simple model, the shift from 2-1 rule to 3-1 rule discourages teams somehow to play the more defensive distribution (2,2) and encourages the more offensive distribution (1,3).
How would the analysis of the static 9-rounds DMA Soccer be more complicated? Well, instead of having 10 sub-outcomes, we would have the 55 sub-outcomes 0:0, 1:0, 2:0, 3:0, 4:0, ... 0:8, 1:8, 0:9. The probabilities attached to them would not look that much different. But then a win for Ann can be obtained in 25 different ways, and a draw in 5 different ways, therefore the probability of a win for Ann would be the sum of 25 terms, and for a draw the sum of 5 terms. All this is not totally out of reach.
In continuous DMA soccer, you assign percentages to defence, midfield, and attack. The three percentages should add up to 100%. Continuous DMA soccer is DMA soccer where the players can be "cut into parts" arbitrarily.
How many different strategies --- distributions of the players into the three parts of the fields--- does each team have?