Polyhedra and Planar Graphs I

Polygons, including the Art Gallery Problem, should have been treated before

Polyhedra

Class Activity: The class starts by distributing a set of paper or plastic polygons. The task is to stick these polygons together at common edges to create closed 3-dimensional shapes, so-called polyhedra. Note that edges that are glued together must have the same length, and at each edge just two polygons are glued together.

Here ares some examples. The empty red triangles in the third example still count as faces.

The flat polygons used as sides of the polyhedron are called the faces. The lines where different polygons are glued together are called the edges. Finally, the vertices are the ends of the lines, the "corners" of a polyhedron. The numbers of faces, edges, and vertices of a polyhedron are usually abbreviated by the letters F, E, and V. Note that the plural of "polyhedron" is "polyhedra".

For the moment, let us define polyhedra as follows: A polyhedron is a three-dimensional object created by putting flat polygons together such that two polygons are joined by a common edge, and every edge bounds two polygons. Obviously every polyhedron could also be viewed as a graph, since we have vertices---the vertices of the polygons--- that are connected by edges. The degree of a vertex in the polygon is the number of edges it is incident with. It is the same as the degree in the graph-theoretical sense.

Let us call the degree of a face the number of edges bounding it. For some famous polyhedra, all faces have the same shape---they are regular n-gons for a fixed value of n. This is true for the five Platonic Solids, where all faces are regular polygons of only one shape, and every vertex has the same degree.

Name (click for animation) Tetrahedron Cube Octahedron Dodecahedron Icosahedron
Look
degree (number of faces or edges) at each vertex 3 3 4 3 5
V=number of vertices 4 8 6 20 12
E=number of edges 6 12 12 30 30
F=number of faces 4 6 8 12 20
degree (number of edges) of each face 3 4 3 5 3

Historical Note: The platonic solids were important to the Greek and Renaissance mathematicians. Plato matched fire, earth, air, water with tetrahedron, cube, octahedron, icosahedron. Kepler tried to find a relation between the 5 known planets and the 5 platonic solids.

Since polyhedra are also graph, we know from the graph page:

Theorem 1: Twice the number of edges equals the sum of the degrees of all vertices in every polyhedron.

Therefore the number of edges doesn't have to be counted but can be computed from the other parameters. In particular, since the graphs of Platonic solids are r-regular, (all vertices have the same degree r) we know that 2E=rV for them, i.e. E=rV/2. For instance, for the cube we have 3·8/2 edges, for the icosahedron we have 5·12/2 edges.

We want to be able to compute the number of edges also for non-Platonic polyhedra, i.e. for nonregular graphs. For this purpose we use the abbreviation of Vn for the number of vertices of degree n in every polyhedron, and in the same way Fn for the number of faces that are n-gons (bounded by n edges). Note that no vertex can have degree 2 in a polyhedron (Why not?)(although in a general graph it can) and of course, there are no 2-gons. Therefore V2 and F2 are always both equal to 0. Of course, since every vertex and every face have exactly one degree, V = V3+V4+V5+... and F = F3+F4+F5+... .

Now the sum of all degrees of all vertices equals 3·V3 +4·V4+5·V5+ .... . Therefore the above remark can be restated as:

Corollary 1: In every polyhedron 2E = 3·V3+4·V4+5·V5+ .... .

We have a similar theorem, this time adding the degrees of the faces. Recall that the degree of a face is the number of edges bounding it.

Theorem 2: Twice the number of edges equals the sum of the degrees of all faces in every polyhedron.
Proof:If we consider all faces one by one, and count all its edges for every face, we have counted every edge twice at the end, since every edge sits between two faces. This is another example of double counting.

Corollary 2: In every polyhedron 2E = 3·F3+4·F4+5·F5+ .... .

Check the previous two Theorems in the data shown below for some polyhedra, and the data for the five platonic solids. Do you see another pattern? Make a table of vertex number versus face number for polyhedra with 12 edges.

Name  doghouse double pyramid Napoleon's hat   UFO  
Look
The base is considered to be one 6-gon, instead of six triangles.
V3,V4,V5.... 6,3 2,3 2,2,2 2,5 0,6,0,2 6,0,0,1
V=number of vertices 9 5 6 7 8 7
E=number of edges 15 = (3·6+4·3)/2 = (3·5+4·0+5·3)/2 9 = (3·2+4·3)/2 = 3·6/2   12 = (3·2+4·2+5·2)/2 = 3·8/2  13 = (3·2+4·5)/2 = (3·6+4·2)/2 18 = (3·0+4·6+5·0+6·2)/2 = 3·12/2    12 = (3·6+4·0+5·0+6·1)/2 =(3·6+4·0+5·0+6·1)/2 
F=number of faces 8 6 8 8 12 7
F3,F4,F5,... 5,0,3 6 (all triangles) 8 (all triangles) 6,2 12 (all triangles) or: 6,0,0,1
      nonconvex     self-dual

Plane and Planar Graphs

A graph is plane if it is drawn in such a way that different edges don't meet each other, except at vertices they have in common, of course, where it is unavoidable. Note that edges don't have to be straight lines here, just curves, although with a little effort, by redrawing the location of the vertices, we can draw every plane graph even with straight edges in this way. Below three examples are given:

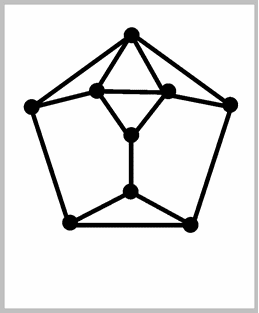The edges of any plane graph cut the plane into pieces. These are called the regions or faces of the plane graph. One of them is unbounded, the outer region.

Theorem 3: Euler's Formula for Plane Graphs: V-E+R=2 for every connected plane graph, where V denotes the number of vertices, E the number of edges, and R the number of regions including the outer region.
  1. Triangulate inside every region which is not one already, draw diagonals until you only have triangles. The number V+E-R remains invariant during this process, since V remains constant, and both E and R increase by 1 in each step. R increases since the graph was connected (otherwise connecting vertices without path between them would not increase the number of regions).
  2. Then remove triangles one by one that touch the unbounded area. There are two cases (the triangle touches the unbounded region with 1 or 2 edges)
    • If it touches the unbounded region with one edge, V remains constant, but E and R decrease by 1.
    • If it touches the unbounded region with two edges, then V decreases by 1, E decreases by 2, and R decreases by 1.
    Therefore in each case V-E+R remains invariant. At the end we have the triangle with V=3. E=3, R=2.

Since V-E+R didn't change during the steps in (1) and (2), V-E+R=2 also for the initial graph.

This formula is not true for non-connected plane graphs, see the graph to the right, which has 8 vertices, 8 edges, and 3 faces.

Graphs may be drawn in different ways, some of them plane, some not. Thus we call a graph planar if it allows a plane representation.

The graphs of polyhedra are planar, aren't they?

Since polyhedra are 3-dimensional, and as such rather difficult to display, we aim at a good 2-dimensional visualization. Actually, by making all faces transparent, we "see" the graph. Vertices and edges are clearly visible, but not the faces. We would like to "see these faces as well. A good plane projection of a polyhedron is a plane drawing of its graph in such a way that the regions of the graph correspond exactly to the faces of the polyhedron. The "good" should remind us that we require more than just the graph made plane.

Further Reading:

Exercises

  1. You glue two octahedra together along a face. How many vertices, edges, and faces does the resulting polyhedron have. What are the degree of the vertices? Why is the resulting polyhedron not Platonic?
  2. How many vertices, edges, and faces does the truncated icosahedron have? Wjy is it not a Platonic solid?
  3. How many vertices, edges, and faces does the truncated dodecahedron have? Wjy is it not a Platonic solid?
  4. Draw the graph of the truncated cube. Draw also the graph of the dual of the truncated cube. How many vertices, edges, and faces does the dual of the truncated cube have?