Shubik Auction II

Prerequisites: Chapters 1, 3, 4, 5, and 6.

This is a continuation of Shubik Auction I. Remember that there, knowing the maximum number of moves in advance leads to the slightly disappointing solution that the player who will eventually not have the last move will not even start bidding, when playing optimally. But what happens if the number of possible bidding rounds is finite but unknown in advance? Or if then number of rounds is finite, but after every move the game could randomly end?

This chapter is mainly an exercise for simultaneou games with randomness, but it also discusses already the connection to games with nonperfect information, and even the connection to games with incomplete information.

• 1. Possible Sudden End
• 2. Imperfect or incomplete Information
• 3. Three players (optional)
• 4. The auctioneer enters the game (optional)

What happens if we don't know in advance which player has the last move? Assume that there is still a maximum number of rounds, but the game could terminate after each round with a given fixed probability p. This makes the game fairer, more profitable for the auctioneer, and also much more interesting.

Of course, for p=0 we just get the non-random version discussed above. How does the backwards induction analysis change?

Let us look at a concrete example SHUBIK AUCTION(35,35,6,0.5). The game tree is shown below, already with expected payoffs for the positions and recommended moves obtained from backward induction analysis filled in. In Beth's last position, she will bid 60. That implies that the expectations at this position for Ann and Beth are -50 and -25. Therefore the expectations at the last random position are the averages of (-50,25) and (-15,-40), namely (-32.5,-32.5). Since -30 is larger than -32.5, Ann passes instead of bidding 50. Proceeding this way, we get expected payoffs of 7.5 for both players at the beginning of the game.

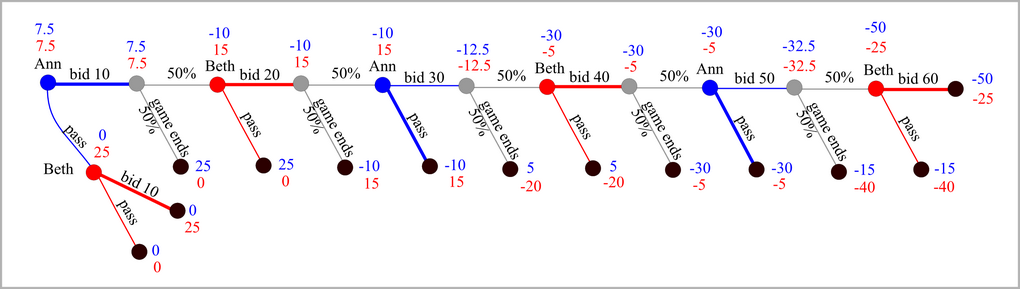
Note also that Ann plays slightly different than in the case without the possibility of a random ending. Like there, she will usually not bid, with the one exception of her very first move. What might be the reason for this change? Well, there is a large possibility that the game ends right after this first bid, and Ann gets the item, and bidding is still cheap at this very beginning.

Is it possible to try the analysis not only for concrete parameters, but once and for all for arbitrary parameters A, B, and p? Of course, for fixed n=6, the structure of the game tree remains the same, and the payoffs can be expressed in terms of A and B, as shown below. Ann's positions are labeled as A1, A2, A3, Beth's positions as B1, B2, B3, and B4, and the random move positions as R1, R2, ... .

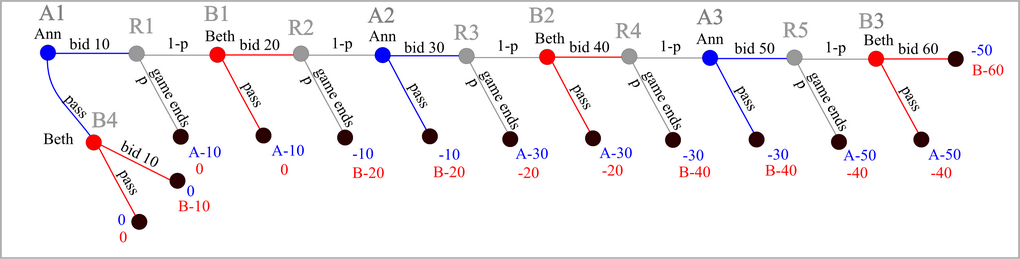
• In position B3, Beth faces payoffs of B-60 versus -40, so she will bid 60 provided B-60 > -40, i.e. B > 20.
• The expected payoffs for Ann and Beth when facing the random position R5 are (1-p)(-50) + p(A-50) = pA-50 for Ann and (1-p)(B-60) + p(-40) = (1-p)B+20p-60 for Beth if B > 20. If B ≤ 20, they are A-50 and -40.
• Next is position A3. If B > 20, Ann faces an expected payoff of pA-50 and a payoff of -30. The first number is larger for A > 20/p, therefore Ann will bid then. If B ≤ 20, Ann bids for A > 20. Therefore, Ann's and Beth's expected payoffs in position A3 are
  • pA-50 and (1-p)B+20p-60 if B > 20 and A > 20/p,
  • -30 and B-40 if B > 20 and A < 20/p,
  • A-50 and -40 if B ≤ 20 and A > 20,
  • -30 and B-40 if B ≤ 20 and A < 20,
  In case B > 20 and A=20/p we get a tie, and it is not totally clear what Beth's expected payoff would be in that case. So we omit this singular case, as well as the case B ≤ 20 and A = 20.
• The second and fourth case could be combined. Thus, the expected payoffs in position R4 for Ann and Beth are
  • (1-p)(pA-50) - 30p and (1-p)((1-p)B+20p-60)+p(B-40) if B > 20 and A > 20/p,
  • -30(1-p)) -30p and (1-p)(B-40)+p(B-40) if either (B > 20 and A < 20/p) or (B ≤ 20 and A < 20),
  • (1-p)(A-50) -30p and -40(1-p)+p(B-40) if B ≤ 20 and A > 20.

For instance, select the 6-rounds sheet and input A=35 and B=35. We get the chart below to the left. Obviously the lines jump at some values of p. In our example, these are around p=0.28 and around p=0.57. These are the values where Ann's or Beth's optimal strategies change. For p between 0 and 0.28 Ann will always pass and Beth always raise the bid. For p between 0.28 and 0.57 we get the same pattern as above for p=0.5: Ann bids 10, but doesn't try higher bids, whereas Beth always bids. For larger p, both will always bid. The probability for a sudden end is just high enough making daring a bid worthwhile. Note that Ann's strategy changes around p=0.28 and around p=0.57, but it is Beth's payoff that dramatically changes at these values.

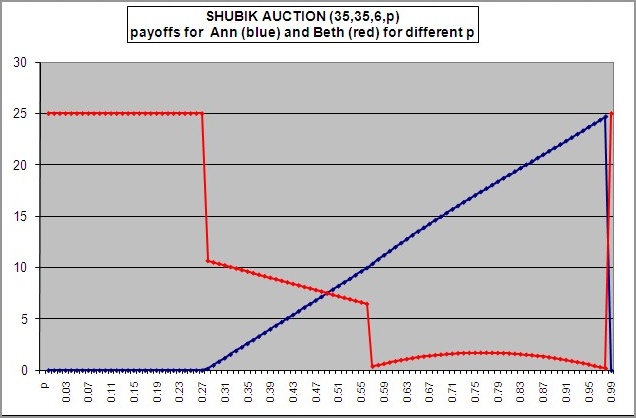
If Ann values the item more, let's say A=45, Ann will obviously try harder to get the item. We get the chart above to the right, which now has 4 strategy patterns. For p between 0.45 and 0.55, Ann always bids, whereas Beth would pass on her 20 bid (while still prepared to bid 40 and 60, but of course, these positions will not be reached then). This strange behavior has to do with Ann bidding for smaller p, due to the higher worth of the item for Ann, whereas this middle level p is not promising enough payoff for Beth, given the relatively low worth of the item for Beth.

Let us play a different variant now, a variant where Nature, instead of deciding after every move whether the game should be terminated, makes this decision when to terminate the game at the beginning of the game, but doesn't tell this decision to Ann and Beth. So we have a maximum number of n moves, and the game starts with a random move deciding the actual number of moves that will be played. Further assume that with probability p₁ this number will equal 1, with probability p₂ this number will equal 2, and so on. Obviously this probabilities must add up to 1, p₁+p₂+...+p_n=1.

Since this random move about the actual number of moves played is not revealed to Ann and Beth, this game is a simultaneous game with randomness and imperfect information. On the other hand, it is rather obvious that for appropriate parameters p₁,p₂,...,p_n this new game is just our SHUBIK AUCTION(A,B,n,p). Since the probability that SHUBIK AUCTION(A,B,n,p) ends after the first round is p, that it ends after the second move is p², and so on, we have to select p₁=p, p₂=p², ..., p_n-1=p^n-1, and p_n=p^n-1. Below is the extensive form of the game equivalent to SHUBIK AUCTION(35,35,6,0.5).

We can even describe this new, more interesting game as a game of incomplete information. We play at most n rounds, but it could be less. Note that incomplete information means that the extensive form is not fully known to the players.

However, in games of incomplete information players need "beliefs" about the structure of the game---without such beliefs, players would not be able to make any decisions. If we assume that both players have the same beliefs about how likely the length of the game is 1, 2, ... n moves, then we arrives exactly at the game of imperfect information discussed above. Only in case of different beliefs, we could not model the game in this way.

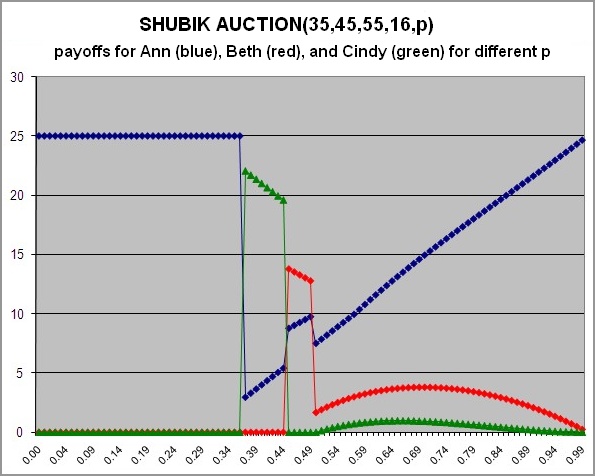
Again this game can be analyzed using an Excel sheet. The different payoffs for optimal play for a fixed example and variable probability p are shown below. Again, the probabilities where one or more of the players change their strategies are rather visible from the graph.

Of course, again it depends on the parameters A, B, and probably to a lesser extend on n. But note that p is no longer a parameter of the game, it is chosen within the game.

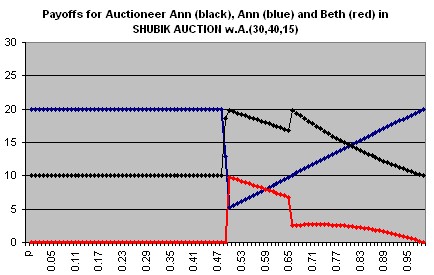
As can be seen from this chart, the Auctioneer should choose p slightly larger than 1/2 or slightly larger than 2/3 to obtain an expected payoff of almost 20 dollars.

References

• Martin Shubik, The Dollar Auction Game: A Paradox in Noncooperative Behavior and Escalation, The Journal of Conflict Resolution, 15, (1971) 109-111.
• Dollar Auctions, a Wikipedia article at http://en.wikipedia.org/wiki/Dollar_auction.

Exercises

1. Below is the graph of SHUBIK AUCTION (45,35,14,p). Are the payoffs identical to SHUBIK AUCTION(43,35,6,p)? Explain.
   
   
   Show/Hide solution
   ...........
2. Find the precise values p for SHUBIK AUCTION(35,35,6,p) where Ann's or Beth's payoffs "jump". Do the same for SHUBIK AUCTION(45,35,6,p) and SHUBIK AUCTION(45,35,14,p)
   
   Show/Hide solution
   ...
3. Can you explain why, when increasing the probability slowly and at some point of p Ann's strategy changes, Ann's payoff remains about the same but Beth's payoffs jumps?
   
   Show/Hide solution
   ...
4. Consider the version of the imperfect information variant discussed in Section 2, where there is a random and secret decision before the game starts whether to end after 1, 2, ... 7 rounds, and where each one of these options has equal probability 1/7. Formulate the game as a game with perfect information, where after the first round the game ends with probability p₁, after the second round with another probability p₂, and so on. How large are p₁, p₂, ... .
   
   Show/Hide solution
   ...
5. Project: Consider the version of the imperfect information variant discussed in Section 2, where there is a random and secret decision before the game starts whether to end after 1, 2, ... n rounds, and where each one of these options has equal probability 1/n. The game can also be formulated as a game with perfect information, where after the first round the game ends with probability p₁, after the second round with another probability p₂, and so on. How large are p₁, p₂, ... , depending on n?
   Modify the Excel sheet ShubikAuction.xls such that these games, for various maximum game length can be modelled. Explore a few cases.
   
   Show/Hide solution
   ...
6. Project: Consider SHUBIK AUCTION(A,B,14,p), where 20 ≤ A ≤ B. Will Beth ever pass?
   
   
   Show/Hide solution
   ...
7. Project: As discussed above, SHUBIK AUCTION(45,35,6,p) has four strategy patterns. Can you find parameters A, B, n, and p where there are 5 or more different strategy patterns?
   
   
   Show/Hide solution
   ...
8. .....
   
   Show/Hide solution
   ...
9. .....
   
   Show/Hide solution
   ...
10. .....
    
    Show/Hide solution
    ...