Every edge connects two vertices. In plane graphs, every edge (actually almost every one) separates two regions. The concept of the dual interchanges the roles of vertices and regions as follows: Inside every region of G (including the outer region) we choose one point, the "capital" of that region. Capitals of regions with a common edge are connected by an edge. This edge should only meet the two regions in question---if necessary, we can also draw the edge curved. Click on the "dualize" buttons below the graphs given above for illustrations. Note that the dual of a plane graph is also a plane graph. Clicking the button again we get the original graph. The dual of the dual is the original plane graph, or at least, it can be transformed into the original one by dragging vertices and edges slightly.
 |
 |
 |
This is the big picture, but there is one fine point to consider:
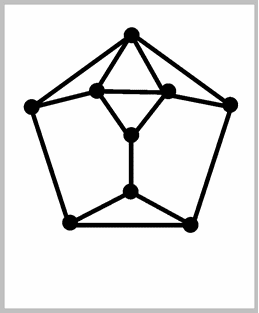
What is there is an edge that does not separate different regions,
like in the example to the right?
We need a property that is a little stronger than being connected.
We call a connected graph 2-edge connected, if
every edge lies between different regions. We only take duals
of 2-edge connected plane graphs.
Start with any polyhedron. The middle of each face will become a new vertex. Now connect those new vertices by straight lines---the new edges---provided the corresponding faces share an edge. We get another polyhedron, having as many edges as the old one, as many vertices as the old one had faces, and as many faces as the old one had vertices. The dual of the cube is the octahedron, and the dual of the dodecahedron is the icosahedron. The tetrahedron is its own dual. The dual of the dual is the old poyhedron.
Note that the dual of a polyhedron with regular faces does not have to have regular faces. An example is the doghouse polyhedron
Since polyhedra are 3-dimensional, and as such rather difficult to display, we aim at a good 2-dimensional visualization. Actually, by making all faces transparent, we "see" the graph. Vertices and edges are clearly visible, but not the faces. We would like to "see these faces as well. A good plane projection of a polyhedron is a plane drawing of its graph in such a way that the regions of the graph correspond exactly to the faces of the polyhedron. The "good" should remind us that we require more than just the graph made plane.
The three graphs above are good plane representations of the doghouse polyhedron, of the cube, and of the dodecahedron.
On the other hand, let us check whether the three plane graphs shown below are good plane projections of the polyhedra obtained from two tetrahedra by identifying one vertex, identifying one edge (the red one), and identifying one face (the red triangle).
The first one is not "good". The outer region of the graph does not correspond to a face of the polyhedron, whereas two faces of the polyhedron do not correspond to regions. The second one is not good either: Again the outer region of the graph does not correspond to a face of the "polyhedron", but two faces are not seen as regions. Only the third graph is a good plane projection of the polyhedron. The red glueing face is no longer a face---after glueing it lies inside the polyhedron.
But wouldn't we obtain a good plane projection for any (?) polyhedron in the following way: First we select one of the faces, and make it transparent. Then we place our camera (using a 360° lens!) in the middle of this face. Now we see all faces, vertices, and edges from inside. What we see is a plane graph, and the regions of it are just the faces of the polyhedron.
It was conjectured by Descartes that V-E+F=2 for every polyhedron. But he didn't give a proof.
Euler wrote two papers on the subject, appearing in 1750 and 1751. He called faces "hedra", therefore the name "polyhedra". In the two papers he proved the the two Theorems and Corollaries expressing twice the number of edges in polyhedra. on the previous page. Then he also stated that V+F=E+2 for every polyhedron, but admitted: "I have not been able to find a firm proof of this theorem." In his 1751 paper, Euler gives a proof for special, convex polyhedra, described later. However, even this proof, for a correct statement, was faulty.
The issue was nagging at mathematicians for some time. Then in 1811, Lhuilier, proved the theorem wrong, while Cauchy in 1813, proved it right. How can that be? How can something be proved right and wrong?
Next we looked at some polyhedra, that appeared soon after the proof and wouldn't obey the formula.
The Crested
Cube. It has 16 vertices, 24 edges, but only 11 faces (the bottom of the smaller
cube is no face), resluting in V-E+F=3. We discussed what was different to
the polyhedra we have seen before. The ring-shaped face (upper part of the
larger cube) looked suspicious, so maybe we don't allow faces with holes,
since such faces are not polygons?
This example could be fixed by drawing two diagonals
on the suspicious face, thereby cutting it into polygons. For this fixed
version, V=16, E=26, F=12, and V-E+F=2 as desired.
The Frame, even when front
and back are divided into two faces each (to obey the "no-holes-in-faces"
condition). We get 16 vertices, 28 edges, and 12 faces, with V-E+F=0 now.
Maybe we shouldn's allow such "tunnel holes" in polyhedra?So what Cauchy really proved with his proof is the following:
saves the proofs. A body in 3-dimensional space is convex
if for every two vertices the whole straight line connecting these points is also inside the body. None of the
5 counterexamples above is convex.
A little inprecise, a convex polyhedron can also be described as what you get from a potato by peeling it with totally straight cuts until no peeling shows. See the two examples to the right.
Art galleries are geometric objects. The angles, the lengths of the "walls" count. If we stretch or modify the gallery slightly, we may need more or less guards.
Polyhedra are also geometric objects, however, when we talk about polyhedra, we usually disregard many geometric properties. When we talk about "the" cube, we don't care how long the sides are, as long as all sides are equal. When counting vertices, edges, and faces, when looking at the degrees of vertices and faces, when talking about which edge bounds which face, and which edge connects which vertices, we are not really talking about geometrical features. By squeezing, slightly deforming, the polyhedron, these numbers and also the equations between them remain the same.
In contrast to geometrical concepts, like length, angles, and shape, topological concepts only refer to numbers and the relations between. Topology is also called "rubber geometry", since it considers features of geometrical shapes that remain fixed if the shapes consist of rubber and are deformed (without tearing shapes, ripping shapes into parts, or punching holes in them).
Our investigation of polyhedra concentrated on topological features. Note also that graphs and plane graphs are topological objects, not geometrical ones---modifying the edges does not change the graph.