

It is interesting that among the numbers of petals of flowers, the numbers 3, 5, 8, 13, 21, 34, 55, or 89 occur over and over. Here are some examples:
In pre-enlightenment time, these numbers 5, 8, 13, 21, 34, 55, 89, ... might have been considered as "holy numbers", if somebody would have counted the petals and spirals, which apparently nobody bothered to do. On the other hand, other numbers were considered holy and "supernatural", since they seemed to rule nature. Of course (?) nowadays we try to find a cause if patterns occur in nature. In this case, the cause is difficult to detect, only around 1990 biologists found the reason for it in case of spirals in seedheads.
The sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, ... was described by the mathematicican Leonardo da Pisa, whose nickname was Fibonacci (the son of Bonacci). Actually Fibonacci illustrated the numbers using an example of rabbits reproducing themselves. He lived around 1180-1241 in Pisa, and is considered to have been the most famous European mathematician of the middle ages (although Arabic, Indian and Chinese mathematicians of that time were more famous). He was one of the first europeans using the indian-arabic ten digits. For this reason, these numbers are called "Fibonacci numbers". However, according to some sources, the Indian mathematician Pingala described and used these numbers already around 400BC.
The Fibonacci numbers F1, F2, F3, ... can be described by following the rule Fn+2 = Fn+1 + Fn. In other words: Every number of the sequence (except the first two, of course, which are just defined to be 1 and 1) is the sum of the two previous numbers in the sequence.
In the following applet you can generate a pinecone or a sunflower seedhead. Write a number into the "number of seeds" field. type a number between 0 and 1 into the "angle as part of 360" field. Then click the "Read and Do" button, or the "step" button repeatedly if you want to create the pinecone step by step. The pinecone is created by placing a new seed close to the center, and then more seeds going counterclockwise and increasing the distance from the center more and more. Note that you see only one set of spirals, and the pattern doesn't look like in nature, unless you use the number close to 0.61803399 as angle ratio. Only in these case the seeds are very closely packed, you see two sets of spirals, one clockwise and one counterclockwise, and it looks like in Nature. So what is so special about the number 0.61803399?
Fibonacci numbers do not only occur in nature, but many natural questions lead to Fibonacci numbers as answers. Here is an example:
Assume you have two types of train cars---those of length 1 and those of length 2. Let's abbreviate those of length 1 by the letter "a" and those of length 2 by the letter "w". Then "awa", "waa", "aww", "ww", and "aaaa" are the five possible trains of length 4. Note that two such trains are only considered equal if both have the same cards in the same ordering from left to right. Now there are the eight trains "wwa", "waw", "aww", "waaa", "awaa", "aawa", "aaaw", "aaaaa" of length 5, and the 13 trains "www", "wwaa", "wawa", ""waaw", "awwa", "awaw", "aaww", "waaaa", "awaaa", "aawaa", "aaawa", "aaaaw", "aaaaaa" of length 6. This data may indicate the conjecture that there are Fn trains of length n.
We will use a different proof technique than that (Reductio ad Absurdum) we used last time. The new method is called "Mathematical Induction".
First we will show that the statement is true for small cases of n. Actually this has already been showed above.
The next step, the induction step, consists in showing that if the statement we have to proof is valid for all numbers less than a given number n, then it must also be true for that n.
In our case, the key observation is that there are two types of trains: Those whose\ first car has length 1, let's call them "type-1", and those whose first train has length 2, the "type-2" trains.
Now how many type-1 trains of length n do we have? Well, as many as there are length n-1 trains, since there are n-1 units to be combined after the leading (length 1) car. By the assumption, this number equals Fn-1.
In the same way, the number of type-2 trains of length n equals the number of trains of length n-2, which equals by our assumption Fn-2.
Every train obviously has one (and only one type). Therefore the number of length n trains equals the sum of the number of length n trains of type-1 and type-2, which is Fn-1+Fn+2. But according to the recurrence formula for Fibonacci numbers, this equals Fn, and the proof is complete.
This question, using long and short syllables instead of cars, and words instead of trains, was raised and answered by the Indian mathematician Virahanka around 600BC.
Look into ratios of consecutive Fibonacci numbers (just click several times on the button above to create these ratios) 3/2=1.5, 5/3=1.666, 8/5=1.6, 13/8=1.625, 21/13=1.6153, 34/21=1.6190, ... Note that after 20 clicks these ratios more or less stabilize. The resulting number is called F, and is called the "golden ratio".
F can be computed: Express these ratios as compound fractions. Let Rn be the ratio of Rn and Rn-1:
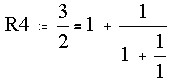 |
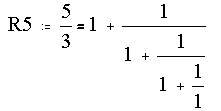 |
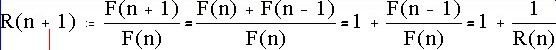
Then F = 1+1/F. Using a little algebra and quadratic equation, there follows that F = (1+sqrt(5))/2 , which is about 1.6190
If we know that the ratio of consecutive Fibonacci numbers equals about F, then we also know that the Fibonacci sequence is about a geometric series, like 1, F, F2, F3, ...