The most natural case for discrete intersection graph models is when all sets have the same cardinality, i.e if we consider intersection graphs of k-uniform hypergraphs.
Line graphs, i.e. intersection graphs of simple 2-uniform hypergraphs, can be recognized easily and quickly. What about intersection graphs of k-uniform hypergraphs for higher k? For motivation, see Example 6.
There is still a Krausz-type characterization:
A graph is the intersection graph of some (simple)
k-uniform hypergraph
if and only if there is some covering of its edges by complete
subgraphs such that every vertex lies in at most k of them
(and no two vertices lie in the same
k
of these subgraphs). |
But what we don`t have for k > 2 is an analogue of this Lemma. Even arbitrary large cliques may be no star graphs, as can be seen for k=3 as follows:
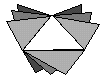
In other words, 3-element sets totally fail the Helly-property. This may be the reason why the case k > 2 is much more difficult than the kase k=2:
Recognizing intersection graphs of k-uniform simple
hypergraphs is NP-complete for every
k  3
[PRT81],
but can be done in linear time for k=2
[R73],
[L74].
Proof |
Large generalized octahedra are not in the class, [P99] therefore maximum cliques can be computed in polynomial time. Therefore, maximum student cliques in Example 6 are easy to find, but note that the members of such a clique do not necessarily all attend the same course.
For every fixed integer k, intersection graphs of k-uniform hypergraphs allow an inexpensive representation of the graph by means of these sets Sx. Note that the union of all these sets Sx contains at most kn elements in that case (where n and m denote the number of vertices and edges), and we may represent elements of this union by log(kn) bits. To store Sx we need k log(kn) bits for every vertex x, thus overall kn log(kn) bits, which is O(n log n) for fixed k. This is less than the space O(n2) necessary for adjacency matrices, or the space O(m log n) needed for neighborhood lists (note that every item of such a neighborhood list requires log n bits), but still we only need a constant number (k2) of comparisons to check whether two vertices are adjacent.
The situation is still different for linear k-unform hypergraphs
Maybe you would like to consider t-intersection graphs of k-uniform hypergraphs, or random intersection graphs, or go back to the start page for intersection graphs.