but
it is allowed that two vertices x,y lying in exactly
t of them, where
t < k, lie in exactly the same.
We could add the one-vertex complete graphs
{x} and {y} to the list in that case.
To
be more precise, the deletions were crossed with point mutations.
A deletion which overlaps a point mutation cannot recombine with it.
Thus deletions and point mutations should form the hyperedges and points
of some interval hypergraph, if the hypothesis of linearity is true.
There
are few exceptions for line graphs:
Coloring, for instance, is still NP-complete
for line graphs (since it is equivalent to edge coloring
arbitrary graphs).
The Hamiltonian cycle problems is also NP-complete for line graphs.
An example of a hard problem even for interval graphs
is ACHROMATIC NUMBER
(Bodlaender, IPL (1989) 135-138).
Me too
wrote this in one of my publications,
and somehow seem to believe in it still---you wouldn't
spend so much time
on a topic you believe intractable.
if
every pair of vertices
in a k-element set S is covered
by some hyperedge, then this set must be a hyperedge
If
W
V and
G = 
((A,
(Sx/x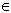 
V))),
then G[W]=(
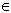(A,(Sx/x W))).
Note
that U is simply the intersection graph of the
hypergraph (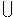
S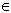
P S, P).
It is here that P being a countable set is required.
This
could also expressed as:
If N[x]=N[y] and if G - x lies in G(P),
then G also.
For the proof, note that you simply have to add
Sx := Sy
to the hypergraph.
For
instance, we might choose all
Sx(i) as subsets of
N
N such that
Sx(i) =
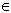{(i,j)/jN}
{(j,i)/ j < i, x(i)x(j)
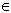E}.
This
is not true for infinite graphs, compare R. Halin,
On the representation of triangulated graphs in trees,
Europ. J. Comb. 5 (1984) 23-28.
where a neighbor of an edge is adjacent
to at least one of its vertices
One way of attacking the
dancing club example consists
in searching for asteroidal triples of edges.
which
can be done in this special
case rather easily, since each
K3,3 lies in a unique biclique
If B contains bicliques containing
K3,4, we choose this as B0.
There are, however, some technical details:
We have to check whether every vertex lies in at most one head of a
biclique and at most one tail of a biclique.
If some vertex does not lie in some head, then we have to add a
artificial pair (
,{v})
which gets a source in D,
and the same for sinks. We may also sample some or all vertices
v1,v2,..., vs
which lie in no head of a diclique,
and instead of adding all these separate new pairs, we add
(,
{v1,v2,...,vs})
they use
completely different terminology.
The theorem has been rediscovered several times, compare
Y. Shibata, On the tree representation of chordal graphs,
J. Graph Th. 12 (1988) 421-428,
but also some unpublished papers by F.V. Jensen, C.E. Carraher,
and myself.
the multigraph
is considered as a weighted graph---every edge has its
multiplicity as weight.
There are,
however, results in this direction which do not use
the weighted-clique-graph-Theorem, see E. Prisner,
Representing triangulated graphs in stars,
Abh. Math. Sem. Univ. Hamburg 62 (1992) 29-41,
for subdivisions of K1,n, and see Ko-Wei Lih,
Ranks of chordal graphs,
Bull. Inst. Math. Acad. Sci. 16 (1988) 357-364,
for trees where there is some subpath such that every vertex
of the tree
has distance at most k to these path.
we also have
Sxt :=
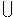{y/ d(x,y)
t-1 Sy.
as the union of Sxt-1 and those S_z
intersecting Sxt-1.
intersection graphs
of trapezoids between two fixed parallel lines.
This is true
for proper circular-arc graphs, compare E. Prisner,
A note on powers and proper circular-arc graphs, JCMCC 1997 .
Choose a maximum matching
M (see J. Edmonds, R.M. Karp,
Theoretical improvements in algorithmic efficiency for
network flow problems,
J. ACM 19 (1972) 248-264),
take all vertices not covered by M into S.
Then it is possible to add for every edge of M
one of its vertices
into S and still maintain independence.
There follows
that there is some
algorithm for the following problem to find H
for intersection graphs
(H) of
large
random
linear 3-uniform simple hypergraphs H.
The algorithm succeeds in finding some such H in almost
every case in polynomial time.
In the few cases where
(H)
7,
either we need superpolynomial time, or we don`t compute H.
Two different
symmetrical vertex-hyperedge incidence matrices for
the same self-dual hypergraph:
The second matrix is obtained from the first one by permuting
the columns as (13651)(24).
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
|
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
|
Since the first matrix has all main diagonal elements `1´, and
the second `0´ on the main diagonal, this hypergraph
can be expressed as the closed-neighborhood hypergraph of some graph
(those whose adjacency matrix is the first matrix, with all entries of
the main diagonal replaced by ´0´),
and also as the neighborhood hypergraph of some graph
(those with the second matrix as adjacency matrix).
Let
G = t(H)
for the hypergraph
H=(A,Sx,x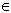V).
Then the sets a*,
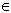aA,
do no longer induce complete subgraphs in G.
Rather every intersection of p of these sets must be complete,
and all these intersections (which are just our star graphs)
cover the edge set of G. Concentrating on these sets
a* has the advantage that properties of H
more easily translate into properties of these sets a*
than into properties of our star graphs.
It has the disadvantage that we have no clue how these sets
a* may look like in G.
There are numeruous examples:
There are characterizations of graphs whose line graphs are
perfect, interval, planar, and so on, see
[P96].
Another question that has received some attention is the question of
which digraphs have interval (or chordal)
competition graphs, compare
[MM99]
...
...
Erich Prisner
made on January 12, 1999,
last changed on February 3, 1999.