Graph Operators
A Java Program by Erich Prisner
Version 0.99, December 1999
- How to get started
- What the program does
- Adjustments at the beginning
- Loading and saving objects
- How to apply operators
- Getting information on the focus object
- Three windows
- Protocol of your session
- Description of the operators
- Inverse Operators
- Hints for beginners
- Basic Definitions
- Some Literature
1. How to get started
Please check the manual
for how to run Java applications on your operating system.
Under Windows 95 for instance, this Java Application can be started by
typing java DFG.Haupt
or
jre DFG.Haupt
in the MS-DOS Prompt, depending on whether you have
the full Java interpreter or only the Java runtime interpreter.
2. What the program does
The program gives an environment to transform
graphs,
digraphs,
and hypergraphs
into each other. No local transformations (like adding
or deleting vertices or edges) are implemented, rather we concentrate
on global operators that see the graph, digraph, hypergraph
as a whole and transform it into another graph, digraph, or hypergraph.
The operators are divided into six groups:
In any case, the resulting object may be graph, digraph, or hypergraph.
Now certain of these operators can be reversed in that way that one
can tell the starting object if one knows only the resulting object
and the operator applied. These "inverse" operators are grouped according
to the end object of the original operator.
At every time, one graph, one digraph, and one hypergraph are present.
One of them is on focus.
Every operator you use applies to the object on focus,
thus only those buttons are enabled that make sense at the moment
(for instance, if we have a graph on focus, then only operators of
group 3 and inverse operators of group 4 are enabled).
However, you may change focus by pressing one of the buttons
"Graph", "Digraph", or "Hypergraph"
(which are rather huge at the beginning).
3. Adjustments at the beginning
At the beginning you may (and should) adjust the main window to your
own needs by adding the operators you need frequently as buttons.
For this, you go to the menu "Buttons", and mark or dismark
the operators, which are grouped in four groups (
1,
4,
2+
5,
3+
6) there.
Certainly you can add or delete buttons in this
way anytime during your session.
4. Loading and saving objects
Although small default start graphs/digraphs/hypergraphs are present
from the beginning, you have to start by loading/creating a
graph/digraph/hypergraph. These options are available under
the "load G", "load D", and "load H" menus. Here you may load
some existing objects (as "Graph1.txt", ... "Hypergraph2.txt")
or objects you have saved previously or in previous sessions
by choosing "..." and typing the file name. See in the subfolder
"Daten" for some graphs, digraphs and hypergraphs. You may also generate
random graphs, bipartite graphs, digraphs, or uniform hypergraphs,
circulants, and certain
Cayley digraphs.
To save an object you have to choose the "Save" button.
You may choose an existing name (as "Graph1.txt") and overwrite
the existing graph stored there, or you may choose an own name
(which should have the form "Name.txt"). Then the object is
stored as a text file in the directory "DFG/Daten". Since the format
for graphs, digraphs, and hypergraphs is different, you should
choose an name which indicates the type of the object.
Since you may want to transfer to other graph programs as
"Graphs and Groups" or "Pajek",
there is the possibilitiy to save your graph in those formats.
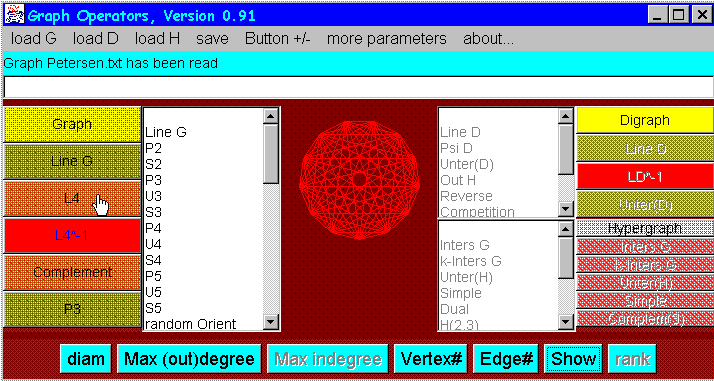
5. How to apply operators
Operators can be applied either by double-clicking on the
corresponding name in the three lists almost in the center of the
main window,
(containing (inverse) operators of type 1 and 4, 2 and 5,
respectively 3 and 6) or, if you have already
created a button
on the main window for the operator, by clicking this button.
6. Getting information on the focus object
The buttons on the bottom of the main window give you some information on the
focus object, such as
diameter (for graphs and digraphs;
if they are not connected respectively not strongly connected, then (somewhat incorrectly)
the vertex number is displayed),
maximum
(out-) degree (for graphs or digraphs),
maximum in-degree for digraphs,
number of vertices or
edges/
arcs/
hyperedges, and
rank (for hypergraphs only).
Some additional features as
minimum degree of graphs,
and minimum outdegree
respectively minimum indegree
of digraphs
are contained in the menu "more parameters".
The information is displayed in the text area on the top of the main window.
Note that computing the diameter may take several minutes if the
graph has 1000 or more vertices.
By pressing the "Show" button, the object is displayed in the
(black) DOS-window as adjacency matrix or list of hyperedges.
If the object on focus turns out to be a graph with no more
than 280 vertices, a
white window
opens and displays a graphical picture of the graph.
Pictures of older graphs are overwritten once
another graph picture emerges.
7. Three windows
Besides the main window there are two other windows visible (under Windows9*).
The white window displaying the present
focus graph after
pressing the "Show" button, and the "black" MS-DOS window.
The Graph Picture can be modified by pressing the mouse near the
vertex you want to move, and releasing the mouse at the new site.
You can also change the size of the vertices and of the numbering
of the vertices. No sophisticated graph drawing algorithms are
implemented---for these we refer to other existing graph programs.
The third (DOS) Window may also contain some useful information at times,
for instance, if you press "show", the adjacency
matrices or hyperedge lists are shown there.
Also at complicated computations, intermediate objects are
shown there. Although the presentation there is rather messy
(and German) it may be of some use at times.
|
.gif) |
8. Protocol of your session
In the file "DFG/Daten/Protokoll.txt" there should be all displays
made during the session. However this feature only works if you
exit the program by the close button, not if you apply Strg-Alt-C
in the MS-DOS window.
The older protocol is overwritten, so if you are interested
in keeping one, you should rename it just after that session.
Examples of such protocols are in "DFG/Daten/Proto1.txt" and
"DFG/Daten/Proto2.txt".
9. Descriptions of the operators
Graph Operators
- LineG: The line graph of a graph G has its edge
set as vertex set. Two former edges are adjacent
vertices in L(G) if they share an edge.
- S2, S3, S4, S5:
The k-sequence graph Sk(G) of a
graph G is defined as follows. The vertex set is the set of all
k+1-tuples (x0,x1,¼,xk) where each pair xi, xi+1 forms
an edge in G. Two such vertices (x0,x1,
¼,
xk) and
(y0,y1,¼,y
k) are adjacent in Sk(G) whenever one can be
obtained by the other by a left or right 'shift', i.e. if either
- xi = yi+1 for each 0
£ i £ k-1, or
- yi = xi+1 for each 0 £ i £ k
-1, or
- xi = yk-i
-1
for each 0 £ i
£ k-1,
or
- yi = xk-i
-1 for each 0
£ i
£ k-1.
- U3, U4, U5:
The graph Uk(G) is the subgraph of Sk(G)
induced by all
vertices (x0,x1,¼,xk) where xi ¹ xi+1for all 0 £ i £ k-2. In other words, no
'U-turn' is allowed in the sequence.
- P2, P3, P4, P5:
The k-path graph Pk(G) of a graph
G has all length-k
paths of G as vertices.
Two such vertices are
adjacent if the union of the corresponding paths is a path or
cycle of
length k+1, and the intersection is a length-(k-1) path.
In other words, it is the subgraph of Sk(G) induced by all
sequences (x0,x1,¼,xk) that are paths.
- random Orient: Every edge of the graph is oriented randomly.
This is no graph operator, since it is not
deterministic, but it is sampled here anyhow.
- K3-H, K4-H: The hypergraph having all complete subgraphs
with 3 vertices, respectively all complete subgraphs
with 4 vertices as hyperedges.
- L3, L4: The k-line graph Lk(G) of a graph G has all
complete k-vertex subgraphs as vertices. Two such vertices
are now adjacent (in Lk(G)) if they have
(as subgraphs in G) a common vertex. In other words,
L3(G)
and L4(G) are the
intersection graphs of the hypergraphs
K3-H or K4-H of G. See the remarks
below.
- If we transform a graph G by G(2-in-3) or G(3-in-4),
we take all edges respectively triangles of G as vertices.
Two such vertices are adjacent if the corresponding edges respectively
triangles of G are contained in some common triangle respectively
K4. Obviously G(2-in-3)(G) and
G(3-in-4)(G) are subgraphs of L(G) and L3(G).
- The Bigraph B(G) of a graph with vertex set
V is the bipartite graph with two disjoint copies
V and {x¢/x
Î V} of V as vertex set.
There is an edge between x Î
V and y¢,y
Î V if either
x = y or {x,y} is an edge in G.
- For the operators Square, Cube, Step2, T2,
PStep3, and the
Complement, the vertex set is the same than in G.
There is an edge between distinct vertices x and y
- ... in the Square if the distance between
x and y is at most 2 in G,
- ... in the Cube if the distance between
x and y is at most 3 in G,
- ... in the 2-step graph Step2(G) if x and y are the
end vertices of some length-2 path in G,
- ... in the 2-distance graph T2(G) if the
distance between x and y equals 2,
- ... in the 3-path-step graph PStep3(G) if x and y are the
end vertices of some length-3 path in G,
- ... in the Complement if {x,y} is no edge in G.
Obviously the complement of the complement
equals the original graph.
Inverse
Graph Operators
LG^-1: The inverse of the line graph LG.
- Pk^-1: The inverse of the k-path graph operator Pk.
- UL^-1: If the graph is the underlying graph
of some line digraph, this inverse operator outputs
the original digraph (in most cases).
- I(t,k)^-1 If the graph is the t-intersection
graph of some k-uniform hypergraph, this hypergraph is (in most cases) found.
- L3^-1, L4^-1: The inverses of the operators L3
and L4.
- G(2-in-3)^-1, G(3-in-4)^-1: The inverses of the operators
G(2-in-3) and G(3-in-4).
Digraph Operators
- LineD: The {\bf line digraph} L(D) of a digraph D has
the arc set of D as vertex set. There is an arc in
L(D) from (x,y) to (v,z) if y=z.
- Unter(D): We get the underlying graph of a digraph
by forgetting all orientations and getting rid of all loops,
i.e. we have the same vertices, and distinct vertices are
adjacent if there is an arc from one to the other or reverse
(or both) in D.
- Out D: The Out-Hypergraph of a digraph
is the hypergraph with the same vertices than D and all
out-sets as hyperedges. Thereby the out-set of a fixed
vertex x is the set of all vertices y where there is an arc
from x to y.
- Reverse: The reverse digraph of a digraph is obtained by reversing
the directions of all arcs.
- Competition: The competition graph of a digraph is a graph.
It has the same vertex set, and distinct vertices x,y are
adjacent whenever there is some vertex z (which may be x or y)
such that there are arcs from x to z and from y to z. The
competition graph is the
intersection graph
of the Out-Hypergraph of D.
- Irreflexiv: A digraph is irreflexive if it has no loops,
i.e. arcs from x to x. The irreflexive digraph is obtained
by deleting all loops.
Inverse
Digraph Operators
- LD^-1: The inverse of the line digraph operator LineD.
You don't get necessarily the original digraph though, since the line
digraph operator is not injective.
Hypergraph Operators
- k-Inters G: The k-intersection graph
Ik(H) of a hypergraph H
has the hyperedges as vertices; two such vertices are
adjacent if the hyperedges have at least k common elements.
- Inters G: The intersection graph
I(H) of a hypergraph H
is the 1-intersection graph.
In other words, I(H) is the
underlying graph of the
dual of H.
- Unter(H): The underlying graph
of a hypergraph
is the graph with the same vertices than the hypergraph.
Two vertices are adjacent in U(H) if there is some
hyperedge containing both vertices.
- Simple: A hypergraph is simple if every hyperedges
occurs at most one. By pressing this button, the hypergraph
is made simple by deleting all entries except one of
multiple hyperedges.
- Dual: In the dual H*
of the hypergraph, the vertices
correspond 1-1 to the hyperedges of H, and the hyperedges
correspond 1-1 to the vertices of H. A H*-hyperedge
contains a vertex of H* if the corresponding H-vertex
in the corresponding H-hyperedge.
- By H(2,3) or H(3,4)
we transform a 3- or 4-uniform
hypergraph H into a 3- respectively 4-uniform hypergraph as follows:
The vertices are all 2- respectively 3-element subsets of
hyperedges of H. The new hyperedges correspond 1-1 to hyperedges
of H, and a new hyperedge contains all new vertices that are
(as 2- or 3-element sets) subsets of the corresponding hyperedge
of H.
- Complem(3), Complem(4):
The hypergraph Complem(k)(H) of a k-uniform hypergraph
is the complete k-uniform hypergraph on n vertices with just
all hyperedges of H deleted.
- Shift: Consider a k-uniform ordered hypergraph, i.e. all
hyperedges have an ordering of its vertices (i.e. are rather
k-tuples than k-sets). The shift digraph Shift(H)
has the (ordered) hyperedges as vertices,
and an arc from (x1,x2,
¼,xk) to
(y1,y2,¼,
yk) if yi = xi+1 for all 1
£ i £
k-1.
- Multiply Each vertex x is replaced by k vertices
x1, ... xk. Each hyperedge {x,y,z,...}
is replaced by all hyperedges of the form
{xi, yj, zt, ... }.
- Translate
Every hyperedge {x,y,z,...} is replaced by all hyperedges
{x+i, y+i, z+i, ...} with i between 0 and m-1 and all entries
modulo m. As "Complem(3)", "Complem(4)", and "Multiply",
this operator is used to create new "regular" hypergraphs.
If the original hypergraph is a difference family
(as for instance Diff9.txt for m=9 or Diff 41.txt for m=41),
then the translate is a
design.
Inverse
Hypergraph Operators
- H(2,3)^-1, H(3,4)^-1: The inverses of the hypergraph operators
H(2,3) and H(3,4).
10. Inverse Operators
We can divide the inverse operators into three groups:
LG^-1, LD^-1
If the line graph and digraph operators have been applied,
they can be reversed in any case
[L74],
[R73], and
[S82].
But these are the only nontrivial operators known with that property---
all other inverse operators work only under certain circumstances
(The recognition problem is NP-complete in most cases).
Note also that you don't always get the original digraph after applying
the line digraph operator and its inverse, since this inverse is
not unique, uniqueness is only achieved if minimum in- and out-degree
of the original digraph is greater than 0.
Pk^-1, UL^-1:
Recognizing k-path graphs for k >= 2 seems to be difficult;
recognizing underlying graphs of line digraphs is NP-complete in general.
However, if the digraphs have minimum in- and out-degree at least 2,
or if the original graphs have minimum degree at least k+1, these
inverse operators can be efficiently applied, compare
[P97]
[P**].
Computation of these inverse operators may
however take some time.
H(k-1,k)^-1, I(t,k)^-1, L4^-1, G(k-1-in-k)^-1:
All operators in this group use the inverse
operators H(k-1,k)^-1. The problem with H(k-1,k)^-1 is that
the (k-1)-hypergraph of a k-uniform hypergraph
can only be computed if the original hypergraph H is "dense" enough
[P*].
Although almost all random hypergraph obey this denseness, small
hypergraphs do not obey it. On the other hand, all inverse operators
except H(2,3)^-1 and G(2,3)^-1 use I(2,3)^-1.
But I(2,3)^-1 uses a check for K5-e-freeness, which is very
time-consuming. Thus for most of the operators in this group
we have the dilemma that large start objects are not possible
by time reasons, and for small ones the algorithms do not work.
See the hints on which start
objects work best.
11. Hints for beginners
If you start
with random graphs on about 12 vertices and p= 0.38 or p=0.72
and iterate "L3" or "L4", then you will recognize different behavior.
Under L4, you eventually get disjoint unions of K5,
but under L3, you either get small graphs,
(that can be easily described) or they explode. Another interesting
start graph for iterating L3 is the graph GE12.txt.
You may load the graph "GE11.txt"
and look what happens under "PStep3".
All circulants
show interesting behavior under "T2", for
instance try C11(1,2,3), C15(1,2,3,4), C19(1,2,3,4,5),
C23(1,2,3,4,5,6), ... .
Complete graphs or digraphs
are easily obtained as random
graphs and digraphs with edge or arc-probability 1.
You get k-uniform hypergraphs from random k-uniform hyperedges
with many hyperedges (say 1000, for 10 vertices) by using the
operator "Simple". Another convenient way for k=3,4 is to
start with the empty hypergraph (a k-uniform hypergraph
with 0 hyperedges, and going to the complement by pressing
"Compl(3)" or "Compl(4)".
Cycles
are also easy to generate, since they are
circulants.
Recognizing underlying graphs of line digraphs L(D) is possible
for all D with minimum in-and out-degree at least 2 (at least in version 1.0).
Recognizing k-path graphs Pk(G) is possible if the minimum degree
of G is at least k+1. The greatest challenge for the program is to try underlying graphs
of line digraphs of digraphs with all in- and out-degrees equal to 2, or k-path graphs
of (k+1)-regular graphs. Such graphs can be generated for instance
as Cayley digraphs (for instance Cayley(S5,32451,34152) or Cayley(S5,54321,42153))
respectively circulants---one has to check however whether the resulting
graph and digraph is connected respectively strongly connected
(i.e. has diameter smaller than vertex number).
One can test whether a graph is the underlying graph of some
iterated line digraph by pressing "UL^-1" and after that several times "L^-1". Try this
for underlying graphs of iterated line digraphs
of the digraphs "DE6.txt" or "DE7.txt".
Here are some sets of hypergraphs and
graphs on which you can test the validity of the inverse
operators of group 3 without having to wait too long for the computer to finish.
In any case, you start with some very sparse (random) graph or hypergraph,
go to the complement to obtain a dense one, and take this dense object
as start of the operation. After that you apply the inverse operator,
take again the complement, and you should arrive at the sparse
object you had at the very beginning. The reason for starting with
sparse objects is that it is much easier to check whether two sparse
objects are isomorphic than to do the same for two dense objects.
- For "H(2,3)^-1", "I(2,3)^-1", or "I(1,3)^-1"
you need a dense 3-uniform hypergraph to start with.
Start with a random hypergraph with 10 vertices and, say,
about 5 hyperedges. Note the hyperedges (by pressing the
"Show" button---you will want to compare these hyperedges
with the hyperedges you obtain at the end). Press
"Compl(3)", "H(2,3)", "H(2,3)^-1", and again "Compl(3)"
and you should arrive at a hypergraph isomorphic to the start one
in less than a minute.
"Compl(3)", "kIntersection" (with k=2), "I(2,3)^-1", and "Compl(3)"
should also bring you back to the start in the same time.
"Compl(3)", "Intersection", "I(1,3)^-1", and "Compl(3)"
should also work, but "I(1,3)^-1" takes much longer---
about ?? minutes.
- For G(2-in-3)^-1, start with a random graph on 13 vertices
and edge probability 0.1. Let the computer show the graph and
copy the (nicely redrawn) picture. Then you go to the complement
"Complement" and press "G(2-in-3)". By pressing "G(2-in-3)^-1"
you reverse the operation (in about 2 minutes on my computer).
Look at the picture of the complement and compare it to the
original picture.
- To check "G(3-in-4)^-1" you need more time
(about 15 minutes on my system) when you start in a similiar
way with a random graph
on 12 vertices and edge probability 0.05.
You get nice (?) pictures of so-called "de Bruijn and Kautz graphs" as follows:
Start with complete digraphs or irreflexive digraphs with 2 to 6 vertices
(by creating a random digraph with 2 to 6 vertices and arc probability 1
and by pressing (or not) the button "Irreflexiv"). Then press "LineD" a
couple of times, taking care that the resulting digraph has not more than 270
vertices. Press "Unter(D)" to obtain the underlying graph. Then "Show".
A hypergraph is linear if no two different hyperedges
have two vertices in common.
You get kind-of-random linear 3-uniform (4-uniform) hypergraphs
by generating random 3-uniform hypergraphs and pressing "H(2,3)"
("H(3,4)").
Create designs from difference sets
(as Diff9.txt or Diff41.txt) by applying "Translate".
Take the dual and compute k-intersection graphs for various k.
What do you observe?
Basic Definitions
A graph consists of a vertex set V,
together with the edge set E, which is a subset of
the set of all 2-element subsets of V.
Two vertices x and y are adjacent if
{x,y} Î E.
We say a vertex x is incident with an edge
{y,z} if x = y or x = z.
The degree of a vertex is the number of incident edges.
The maximum degree
respectively minimum degree
of a graph is the maximum respectively minimum degree of
its vertices.
A path of length k is a graph with
x0,x1,¼
,xk as vertices and edges
{x0,x1},{x1,x2}
¼{xk-1,
xk}, whereas a
cycle of length k has vertices
x0,x1,¼,xk
and edges {x0,x1},{x1,x2}
¼{xk-1,
xk}, {xk,x0}.
The distance between two distinct vertices in G is the
shortest length of a path in G with the two vertices
at the ends if there is such a path, otherwise it is
¥.
The diameter of
the graph is the largest distance
occuring.
The complete graph Kk has k vertices
and all possible edges between different vertices.
A subset W of the vertex set of a graph G induces
some induced subgraph
G[W]: Its vertex set is W,
and two distinct vertices are adjacent in G[W] if and only
if they are adjacent in G.
A digraph D has a
vertex set V and an arc set A,
which is a subset of V ×V.
If (x,y) Î A,
then vertex y is called an
out-neighbor of x, whereas x is an
in-neighbor of y. The
out-degree respectively
in-degree of a vertex is the number of
our-neighbors, respectively in-neighbors,
and the
minimum/maximum out-/in-degree
of
a digraph
is simply the minimum respectively maximum
out- respectively in-degree occuring in the digraph.
A directed path of length k has vertices
x0,x1, ¼,xk and arcs
(x0,x1),(x1,x2),
¼,(xk-1,xk).
The distance from vertex x to vertex y in D is
the smallest length of a subpath from x to y in D,
provided there is such a path, otherwise it is
¥. The diameter of D is the largest
occuring distance.
A hypergraph consists of a set together with
some hyperedges, i.e. subsets of that set.
The elements of the set are called vertices again.
The rank of a hypergraph is the maximum cardinality of
a hyperedge, and a hypergraph is called uniform if all hyperedges have the
same cardinality. It is simple if all hyperedges are distinct, and linear
if every two hyperedges have at most one common element.
Let a group G and a subset A of elements be given.
The Cayley digraph has the elements of the group as vertices.
There is an arc from x towards y if there is some element a in A
with y = xa.
A circulant digraph Cn(a1,a2,...ak) has n
vertices labeled by 0,1,2, ... n-1 and there is an arc from
vertex i to vertex j if |i-j| = ai (mod n) for some i.
Circulant graphs are just underlying graphs of circulant digraphs.
Some Literature
If you are interested in the details of the algorithms for
the inverse operators, you may find detailed descriptions
in the following papers:
- P.G.H. Lehot, An optimal algorithm to detect
a line graph and output its root graph, J. Assoc. Comput. Mach.
21 (1974) 569-575.
- N.D. Roussopoulos, A max{m,n} algorithm for
determining the graph H from its line graph G, Inform. Process.
Letters 2 (1973) 108-112.
- M.M. Syslo, A labeling algorithm to recognize
a line digraph and output its root graph, Inform. Process.
Letters 15 (1982) 28-30.
- E. Prisner, Recognizing random intersection
graphs, to appear in Discrete Math.
- E. Prisner, Bicliques in graphs II: Recognizing
k-path graphs and underlying graphs of line digraphs, Proceedings
WG97, LNCS 1335 (1997) 273-287.
- E. Prisner, Recognizing k-path graphs, to appear
in Discrete Appl. Math.
Much information on the operators used are contained in the book
- E. Prisner, Graph Dynamics, Pitman Research Notes in Mathematics
No 338 (1995), ISBN 0 582 28696 4.


.gif)