Zn
by fn = 2n (mod n)
(doubling modulo n).
Draw the digraph of the relation.
CMIS 160
a) We define a function
fn: Zn = {0,1,2, ... n-1}
Zn
by fn = 2n (mod n)
(doubling modulo n).
Draw the digraph of the relation.
b) We define another function
gn: Zn
Zn
by gn = n2 (mod n) (squaring modulo n).
Draw the digraph of the relation.
c) Find the range of the functions fn and gn. Find fn(11), gn(11), and fn(fn(11)), and gn(gn(11)).
d) Find the range of the composed function
fn ° fn ° fn ° fn ° fn.
e) Find the range of the composed function gn ° gn ° gn ° gn ° gn.
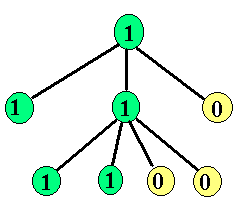
f) Look at the tree shown to the right. How many labeling of the vertices of the tree with 1's and 0's have the property that for every vertex x labeled by 1, all vertices of the path from this vertex x to the root have label 1 too. Such a labeling is also shown in the picture.
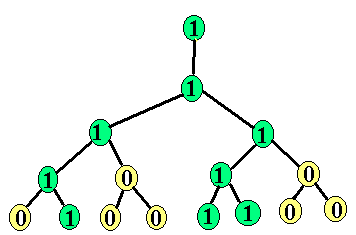g) Answer the same question for the second tree to the right.
h) How many subsets M of Zn = {0,1,2, ... n-1} have the property that fn(M) is contained in M, i.e. that fn restricted to M is again a function from M to M?
i) Similiar, how many subsets M of Zn have the property that gn(M) is contained in M?
j) Answer all questions (a), (b), (c), (d), (e), (h), (i) for n = 15.
Go to Project # 5. 2. Liers
In Wafabia there are only two kind of people. Honest people
who will never lie, and (chronical) liers,
who will never say a true sentence.
Let's listen to some conversation on the market place:
Astrid : Rosi is a lier.
Can you find out who is lying and who is honest if you get the additional information
that out of the 15 people involved, exactly 7 are liers? (Hint: Use bipartite graphs)
Boris : Steffi is a lier.
Steffi : Astrid is a lier.
Rosi : Erik is a lier.
Steffi : Heide is a lier.
Dieter : Jan is a lier.
Grit : Boris is a lier.
Heide : Michael is honest.
Uwe : Lothar is a lier.
Dieter : Rosie is a lier.
Franz : Grit is a lier.
Jan : Uwe is a lier.
Heide : Jan is a lier.
Lothar : Franz is a lier.
Xaver : Jan is honest.
Christel : Grit is honest.
Go back to Project # 3.
Projects differ in certain ways from homework.
They questions there are more complex, more difficult,
have several steps,
and sometimes you have to use notions and tools from several chapters
to solve them. But in most cases, the theorems and tools learned
do not suffice to solve all parts of the project.
Rather you have to discover certain facts by yourself.
Learning how to make "discoveries" in the field is an important
part of the class---in real life you donīt have always a textbook telling you
exactly what to do.
Of course you are encouraged to use any other material---books,
webpages, and so on.