Try the random walk on a path of length 4.
Here the probability distributions:
Let a(n), b(n), c(n), and d(n) denote the probabilities that the the fields are visited in the nth step. If the right field is absorbing, the recurrence formulas are
| a(n)=b(n-1)/2 | b(n)=an+c(n-1)/2 |
| c(n)=b(n)/2 | d(n)=c(n)/2 |
with initial conditions a(0)=1, b(0)=0, c(0)=0, and d(0)=0.
|
|
|
|
When solving this system, we get
.
The characteristic equation for the resulting recurrence relation, -4x2+3=0
has two zeros, 
,and 
,
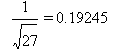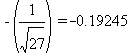and when solving the system of linear equations we obtain, we get
d(n)=
.
Obviously for even n we have d(n)=0, and for odd n we get d(n)=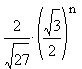
.
For the expected value for the transition time from the leftmost to the rightmost cell, (using a formula for a series) we get
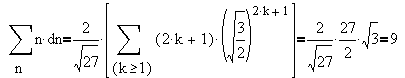
Erich Prisner 2004