MAT37x
Franklin College
Spring2004
Erich Prisner,

Interchanging saddle points and extreme points

The connection (see here for the question) is: Saddle points of one surface correspond to extreme points of the other and vice versa. Climb- or lava-paths of one correspond exactly to saddle-1- or saddle-2- paths of the other and vice versa. But the funny thing is, that the shape of both surfaces is rather different, and also the level lines are quite different. (The relation seems to be more interesting than the obvious one between f(x,y) and -f(x,y), where minimum points correspond to maximum points and vice versa, and saddle points correspond to saddle points. There the level lines are just identical.)

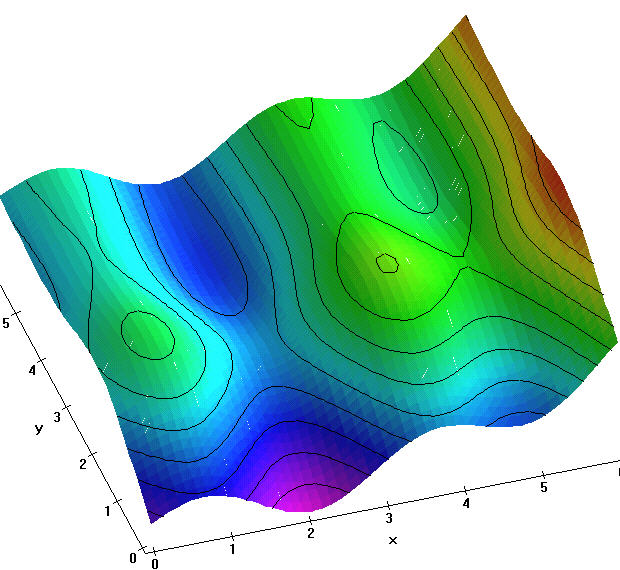Question 1: Does every surface have such a "dual" with the above properties? If not, what are necessary or sufficient conditions for the equation of the function in order to have such a "dual"? Solution

Question 2: Is there only one (up to vertical shift) such dual? Solution

Question 3: What happens if we drop the condition about the correspondence between lava- and climb-paths on the one hand and the saddle paths on the other? So we are only looking for a surface with saddle points, relative minimum and maximum points at some given places. Can you always find such a surface? Try it for relative maximums at (2,2), (2,4), (4,2), (4,4) and a saddle point at (3,3). Solution

Question 4: Investigate the one-variable-version of the relaxed question 3. Is it always possible to find a smooth function from [0,6] to R that has relative minimums at certain x-values, relative maximums at certain x-values, and also fixed points of inflection. Solution

Question 5: Try the following special case of question 4: Find a smooth function f from [0,6] to R with relative minimums at x=2 and 3, relative maximums at x=5, point of inflection at x=4, but no other points of that type. Solution

Question 6: It is well-known that every (continuous) function from [a,b] to R has an antiderivative. Can this be extended to functions with two variables? If g and h are continuous functions from [0,6]² to R, is there a function f from [0,6]² to R such that f_x=g and f_y=h? Which conditions are necessary or sufficient? Solution

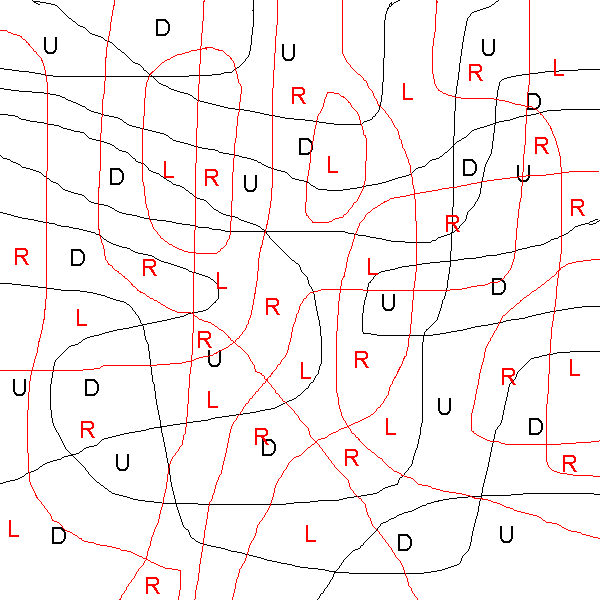
Question 7: A weaker situation: Not f_x and f_y are given, but just their zero curves. That is, we have two (systems of) curves a (the black ones in the picture to the right) and b (the red ones) in the square [0,6]². Is there a function f from [0,6]² to R such that a is the set of all points (x,y) with f_x(x,y)=0, and b is the set of all points with g_x(x,y)=0? Solution

Question 8: Which differentiable functions f of two variables obey f_xy = 0? Solution

Question 9: How do the zero curves f_x(x,y)=0 and f_y(x,y)=0 look like for functions f where f_xy = 0? Solution

Question 10: Solution