MAT37x
Franklin College
Spring2004
Erich Prisner,

What hills, what hills are those my love
That rise so fair and high?
Those are the hills of Heaven, my love
But not for you and I

Skiing and lava on

Example 1

We have a function

Here is a 3D picture of the surface for x and y both between 0 and 6. Have a good look on the surface. Try to identify all hills (relative maximums), sinks (relative minimums) and saddle points. How many of each can you find?

How the applet works

In the applet below, you can play with the surface, thereby investigating it further. First note that you see a topographical map of the surface. The black curves are "streets"---lines of the same height. We call them level lines.

We start by simulating lava streams in Iceland. Press the "lava" button. Click on the map where the lava should start. Click several times (anywhere) on the map to let it run further. You can create up to 50 lava streams. Describe the way of the lava in terms of the level lines. Click until the line goes no further. In what kind of point does this happen.

Now click the "climb" button, the surface where we are to start, and again several times the surface anywhere. What is the resulting curve? Describe it again. What is the difference to the lava line? Again click until the line ends and describe at which kind of point this happens.

Now click the "roll ball" button. Click on the surface to start it, and click again several times anywhere on the surface to continue its way. If the ball moves too quick, reduce speed by decreasing the "factor" (click on the "decrease" button to the right of the "factor" field. What is the difference between the lava lines? Start a lava line and a ball line at the same point and see what happens. Describe the different behavior of lava and balls going down a hill.

Now increase or decrease the "slipperiness" of the snow, and again compare ball and lava. What do you observe for very small slipperiness (like 0.7 or so)?

Unfortunately your browser does not support Java applets.

• the slipperiness indicates the quality of the snow/ice. If it is 1, it is ideal ice and we don't have any friction. If it is close to 0, we don't have snow but rather sand. Then there wouldn't be any movement, because of the high friction.
• the agility denotes the angle the skier can turn between consecutive "moves".
• the stability doesn't mean anything at the moment. Later it will describe at which slope a skier g
• the factor indicates the overall steepness of the whole surface.

Exercises:

1. Find all 10 saddle points of the surface by starting on one of the saddle point buttons and clicking repeatedly on the landscape. After having found a saddle point, start two lava trails downhill untill they end in a sink, and two steepest ascend climb trails until they hit a hill. Solution.
2. ......

The partial derivatives

See 3D views of f_x and f_y here (actually I made the x-y plane a water surface, so only the positive parts of f_x and f_y show):

f:

fx: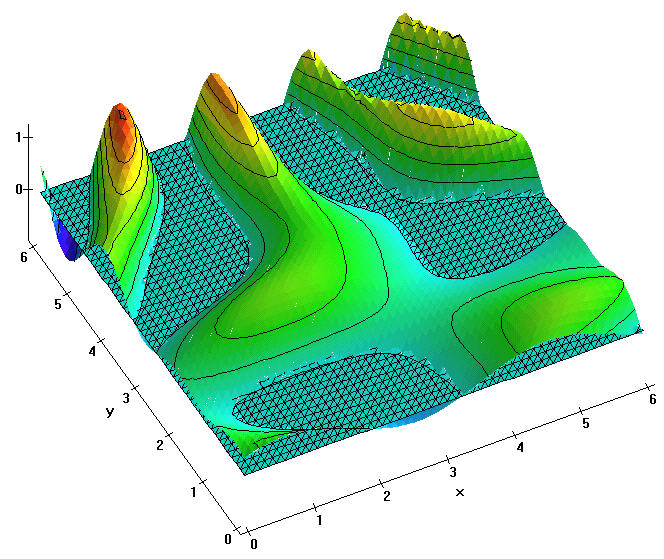

fy: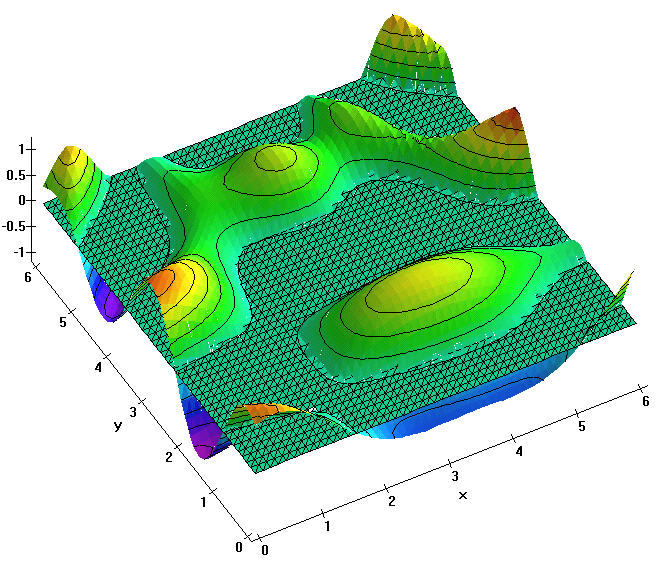

The eight directions

Standing at every point, there are eight natural directions to go. When clicking the "climb" button, the computer moves into the gradient direction (f_x,f_y), wheras with the "lava" button it moves in the opposite direction (-f_x,-f_y). With the "saddle1" button it moves in the direction (f_x,-f_y), and with the "saddle2" button again in the opposite direction (-f_x,f_y).

Sligtly differently works the "street" button, it lets the computer move into direction (f_y,-f_x), creating a level line. The same level lines in the other direction would be created by moving into (f_y,-f_x) direction. But what would happen if the computer would always move into direction (f_y,f_x)? Unfortunately there is no such button on the applet.

The four kinds of areas

What does f_x>0 mean for a point in the original surface? It means that the surface increase when moving in the (positive) x-direction. In other words, at that point one can see the sunset (at least locally, disregardin all hills blocking the view that are farther away. On the other hand f_x<0 means we can see the sunrise (locally). f_y>0 means we have a local view south, and f_y<0 northwards.

The most important part of f_x and f_y are the points (x,y) with f_x=0 or f_y=0. These are the points where the f_x and f_y surfaces touch the "water" x-y plane. Hold your mouse over this link to visualize these lines on the map of the surface. The black lines are the points where f_x=0, and the red lines are those points with f_y=0. Hold the mouse over this link to change the picture back. Here you see the four kind of areas, depending on the signs of f_x and f_y

Gradient

Now the gradient vector is obviously (fx,fy),(see the gradient field here) whereas (-fx,-fy) shows the direction where the steepest descend is. This steepest descend has the slope sqrt(fx^2+fy^2). if the mass is accellerated by factor when falling, we get the accelleration down this steepest descend as ... = (factor*fx/sqrt(slope^2+1),factor*fx/sqrt(slope^2+1)). This is the formula we use for the moving ball, in connection, of course with the Traegheit ...

And what hills, what hills are those my love
Those hills so dark and low?
Those are the hills of Hell, my love
Where you and I must go.
(House Carpenter)