Sometimes players have not a finite number of options but infinitely many.
Very often there are two players who both choose a number between 0 and 1, in which case the
game is called game over the unit square. Instead of the payoff matrix,
the payoff could be visulaiyed by two, or even obne, in case of a zero-sum game,
surfaces over the unit square.
Let there be two players, each one choosing a number between 0 and 1. If Anna chooses y and Beth chooses x (this is not a type, I want to keep the property that Anna chooses the row, the horizontal line, and Beth chooses the column, the vertical line), then the payoff for Anna is x3+y3-xy, whereas the payoff for Beth is just the opposite. The payoff surface for Anna is shown in the picture to the right. How would the players play?
The Maximin Move in
unit square games is found similiar to how it is found in games with finitely many moves,
which can be described by payoff matrices,
except that rows are replaced by horizontal lines.
In the example given above, the first player would mark for each horizontal line
the lowest value, as indicated by the red curve in the graph to the right.
Then player 1 would choose the highest value on this path, which is the point
at (0.6,1), therefore player 1 would choose y=1 when playing the Minimax Strategy here.
The second player would mark for each vertical line the highest value
(since this is the lowest payoff for player 2); the blue curve connects all
these marked points. Then player 2 would choose the lowest (since again, this means highest
for player 2) point on this blue path, which again is the marked point (0.6,1).
Therefore player 2 would choose x=0.6 when playing the Minimax Strategy.
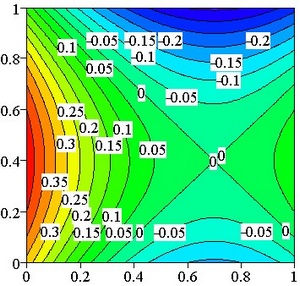Assume there are two players, each one has to choose a number between 0 and 1.
Then the payoff for Anna is x2-y2-1.4x+0.8y+0.33,
whereas the payoff for Beth is just the opposite. How would the players play?