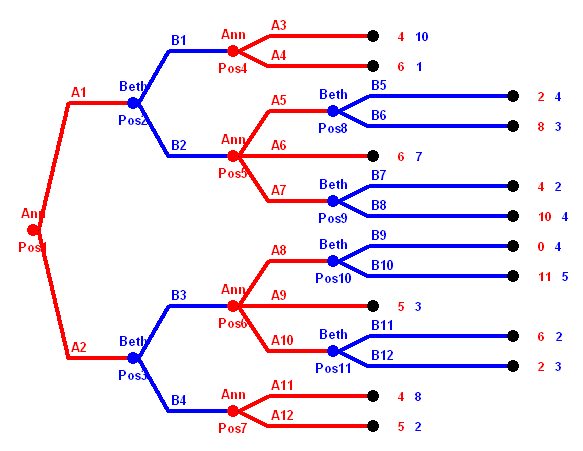
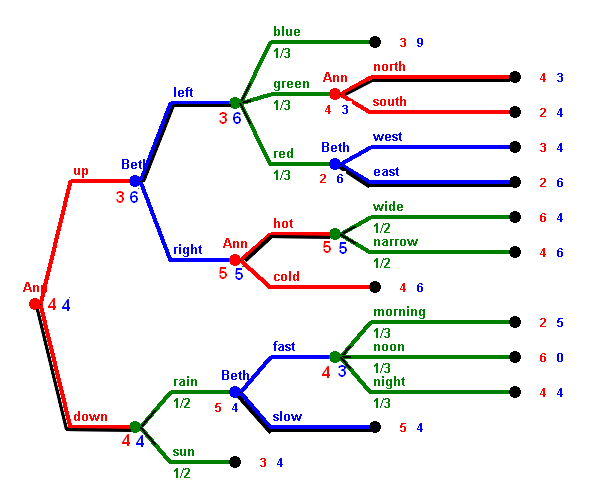
4 · 5 = 20
4 · 3 · 5 = 60.
.........
| L | M | R | |
| U | 1,1 | 3,4 | 2,1 |
| M | 2,4 | 2,5 | 8,1 |
| D | 3,3 | 0,4 | 0,9 |
- Find the Maximin moves for both players.
- Which moves are dominated?
- Find the bimatrix obtained by IESD.
- Find the bimatrix obtained by IEWD.
- Draw the best response digraph.
- Are there any Nash equilibria?
Maximin move is "M" for both Ann and Beth, guaranteeing a value of at least 2 for Ann and at least 4 for Beth.
For Ann there is no domination, weak or strong. For Beth, move "M" dominates (strongly, and therefore also weakly) move "L".
After removing option "L" for Beth, suddenly Ann's move "D" is strictly (and therefore also weakly) dominated by both "U" and "M". After eliminating this option as well, we arrive at the following bimatrix:
| M | R | |
| U | 3,4 | 2,1 |
| M | 2,5 | 8,1 |
| M | |
| U | 3,4 |
The best responses are U-->M, M-->M, and D-->R for Beth, and L-->D, M-->U, and R-->M for Ann.
Therefore the Nash equilibrium is "U" versus "M", since "M" is Beth's best response against Ann's "U", and "U" is Ann's best response against Beth's "M".
SCHEDULING A DINNER PARTY:
Ann and Beth are not on speaking terms, but have a lot
of common friends. Both want to invite these friends to a dinner party this weekend.
Possible are Friday or Saturday evening.
Both slightly prefer Saturday. If both set the party at the same time, this
will be considered a disaster with a payoff of -10 for both. If one plans
the party on Friday and the other on Saturday, the one having the Saturday
party gets a payoff of 5, and the other of 4.
| friday | saturday | |
| friday | -10,-10 | 4,5 |
| saturday | 5,4 | -10,-10 |
DEADLOCK: Two players play a symmetric game where each one can
either cooperate or defect.
If both cooperate, both get an payoff of 1.
If both defect both get a payoff of 2.
If one cooperate but the other defects, the one cooperating gets a payoff of 0,
and the other defecting a payoff of 3.
Draw the bimatrix of the game. Find the Maximin moves,
possible domination, draw the best response digraph, and find all pure Nash equilibria.
| Cooperate | Defect | |
| Cooperate | 1, 1 | 0, 3 |
| Defect | 3, 0 | 2, 2 |
STAG HUNT: Two players play a symmetric game where each one can
either hunt stag or hare.
If both hunt stag, both get an payoff of 3.
If both hunt hare, both get a payoff of 1.
If one hunts stag and the other hare, the stag hunter gets a payoff of 0,
and the hare hunter a payoff of 2.
Draw the bimatrix of the game. Find the Maximin moves,
possible domination, draw the best response digraph, and find all pure Nash equilibria.
|
|  |
CHICKEN: Two players play a symmetric game where each one can
either play Dove or Hawk.
If both play Dove, both get an payoff of 2.
If both play hawk, both get a payoff of 0.
If one plays Dove and the other Hawk, the one playing Dove gets a payoff of 1,
and the other one a payoff of 3.
Draw the bimatrix of the game. Find the Maximin moves,
possible domination, draw the best response digraph, and find all pure Nash equilibria.
|
|  |
...
...