During 1654, Blaise Pascal and Pierre de Fermat exchanged a series of letters. Fermat was at that time 53 years old and judge in Toulouse. He also did mathematics in his spare time with extraordinary success. A former child prodigy, Pascal was 31 years old and living in Paris. In these letters they discuss a problem posed to Pascal by the Chevalier de Méré, a frequent gambler. Pascal made an attempt towards a solution and wrote it to Fermat, probably for confirmation but maybe also for help. We can only guess here, since this first letter is lost.
Developing scientific ideas in letters instead of papers was not unusual at that time. Scientific journals did not yet exist, the first ones appeared only in 1665. Books were written to communicate existing theories, but in order to develop new results, to communicate it to each other, and to gain credit for a new discovery, scientists and mathematicians wrote letters to each other. Actually Pascal and Fermat hadn't met, and addressed themselves rather politely and formally as "Monsieur".
The following question was discussed in these letters: Two players, A and B, decide to throw a coin repeatedly. Head counts for A and tail for B. They decide to proceed until one of them has collected six points, and then the winner would win the stake of 64 units. But now assume the game is interrupted at a certain standing, let's say 4:3. How should the stakes be divided?
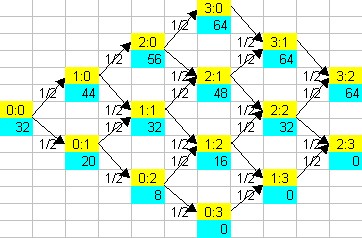For simplicity, we discuss the smaller case where the player first reaching three points wins.
Pascal's concludes as follows: First, it is understood that if the
standing is a draw, like 2:2, or 1:1, or 0:0, then by symmetry both
players should expect the same amount of money, 32 in the example discussed.
Then Pascal considers the case where player A has received two points
and player B one, a standing of 2:1. Now if A would get the next point, A would win,
resulting in a payoff of 64. If B would win the next round, the standing would be 2:2,
an expected value of 32 for each. Since both outcomes have 50% probability,
Pascal computes the expected value for A in this situation as
0.5 × 64 + 0.5 × 32 = 48.
For a standing of 2:0, with 50% probability the next standing
would be 3:0 with a payoff of 64 for A, and with 50% probability it would be 2:1
with an expected payoff of 48 for A, as derived before. Therefore the expected payoff
for A at a standing of 2:0 would be
0.5 × 64 + 0.5 × 48 = 56.
Finally, in the same way the expected payoff for A in the situation 1:0 would be
0.5 × 56 + 0.5 × 32 = 44.
Of course the payoffs at the situations 1:2, 0:2, and 0:1 would just be reversed.
It is certainly not a coincidence that Pascal treats the position 2:1 before treating the position 2:0, and treating that before the position 1:0. The analysis of 2:0 relies on the expected value for the situation 2:1, therefore this value must be known at that time. What Pascal really does is applying backwards induction in a game with only random moves. Here is an Excel file analyzing the originally considered case where 6 points would assure the win.
The above approach has the disadvantage that in order to find some expected values, one has to compute all expected values. Fermat explained how to compute the expected values in an explicit formula. Assume the standing is x:y, where n points are necessary for a win. Then the game would be over after at most 2n-x-y-1 additional rounds, since one of both players, but not both would have the desired n points. Therefore the possible future, what may have happened if the game would have proceeded, can be encoded by a string of 2n-x-y characters of "a"s and "b"s---an "a" if player A would have won, and a "b" if player B would have won. Such a future is good for player A if there are at least n-x "a"s in it, and good for player B otherwise. Note that in some of these possible futures, one player would have won even before all the additional 2n-x-y-1 rounds have been played, but we would play on anyway, just to make the analysis easier (to have all these futures equally likely) ---this was also a argument raised to Pascal when he discussed this approach with other people in Paris. All of these 22n-x-y-1 encodings are equally likely, so each of them has probability 1/22n-x-y-1 Then player A should get k/22n-x-y-1 of the stake, where k is the number of strings with letters "a" and "b" of length 2n-x-y-1 with at least n-x "a"s.
As a result of the letters, Pascal wrote the famous "Treatise on the Arithmetical Triangle", where he had rediscovered and described what is now called Pascal's triangle. This triangle has been described and investigated by Indian, Persian, and Chinese mathematicians before. The construction rule is that on the "roof" you have all "1"s, and each number inside is the sum of the two numbers one row above it---one to its left, one to its right. Here is the top of it, but of course we could easily add more rows below, just using this construction rule.
| 1 | ||||||||||||||
| 1 | 1 | |||||||||||||
| 1 | 2 | 1 | ||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||
The kth entry in row n, called the binomial coefficient "(n-1 choose k-1)" gives the number of strings with letters "a" and "b" of length n-1 with exactly k-1 "a"s. Therefore, Fermat's explicit formula for the expected value for player A in the situation x:y when playing for n wins can also be expressed in terms of Pascal's triangle. You add all numbers to the right of the binomial coefficient (2n-x-y-1 choose n-x+1) and divide by the sum of the whole row. Therefore the simplest nontrivial ratios occurring are 1/4 or 3/4 in row 3, 1/8 and 7/8 in row 4, 1/16, 5/16, 11/16, 15/16 in row 5---the cases discussed in Pascal's and Fermat's letters.
Although this discussion is usually attributed as the birth of Probability Theory, investigations of chance have been done before. The Italian mathematician Girolamo Cardano (who was also involved in the discovery of the cubic and quartic formula, a quite interesting story itself, compare []) has written a "Book on Games of Chance", published in 1525. Here he computed probabilities of simple events, like a die showing a given number, and also of composed events, like the sum of the numbers showing on two dice equals a given number. These results were also independently rediscovered later by Galileo Galilei. But what was new in Pascal's and Fermat's exchange was the idea of expected value. It is also interesting to see how closely the beginning of probability theory was attached to gambling and games of luck. Only much later, when statistics began, probability theory could show its seriousness by providing a solid basis for statistics.
At the end of the year 1654, after some time of severe depression and a mystical experience, Pascal withdraw from mathematical and scientific work and devoted his time with philosophy and theology. In 1960, having learned that Pascal has moved (for several months) to his birthplace Le château de Bien-Assis close to Clermont-Ferrand (which is about 374 km from Toulouse), Fermat initiated contact again in a letter where he suggested a meeting half way between them. In his response letter, Pascal admits that Geometry is "the very best intellectual exercise", however states now that he finds it "so useless". He continues: "Although I call it the best craft in the world, it is after all only a craft, and I have often said it is fine to try one's hand at it but not to devote all one's power to it. In other words, I would not take two steps for Geometry [...]." [Pascal,Fermat 1] That settled the question of a possible meeting.