Analysis of WAITING FOR MR PERFECT II

As in part I, we only consider the two players case, where the awards have value 1, 2 or 3, and appear with probabilities P(1), P(2), and P(3) in each round, independent of the awards drawn in the previous rounds.

1. Mixed Strategies in Two Rounds

How do mixed strategies extend the analysis we have done so far for the two-rounds case?

The case P(2)+2·P(3) < 1

Recall that the bimatrix with strictly dominated moves eliminated looks as follows:

	III	NII
III	c , c	b , d
NII	d , b	a , a

with the four numbers a < b < c < d expressions in P(1), P(2), and P(3). As shown in part I, there are two pure Nash equilibria, namely "III" versus "NII" and "NII" versus "III". However, there is also a Nash equilibrium in mixed strategies. Assume Ann plays "III" with probability p and "NII" with probability 1-p. and Beth plays "III" with probability q and "NII" with probability 1-q. Then pc+(1-p)b=pd+(1-p)a, thus

To compute the expected payoffs in this case is left as an exercise. In the concrete case of P(1)=1/2, P(2)=1/3, and P(3)=1/6, we obtain a= ..., b=..., c=..., d=..., and p=q= ... and the payoffs are ... displayed in the graph to the right. ......

The case P(2)+2·P(3) < 1

After eliminating the strongly dominated strategies, we arrive at the following reduced matrix:

For P(1)=0.2, P(2)=0.3, P(3)=0.5, we get three Nash equilibria, two pure ones of "NII" versus "NNI", with payoffs 2.16 versus 2.25, and one mixed equilibrium of 85% NII versus 15% NNI with expected payoffs of 2.19 for both.

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

...

2. The game is recursive

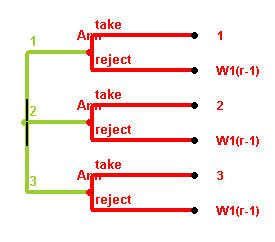Let us call the r-rounds game with n players Wn(r). Note that this is not a number but a game. At the beginning of the k-th last round (except for the first two rounds) we have four subgames, depending on whether both players are still searching, or one of them has already got an award, or whether both have already their award. In the last case we could also declare the game over, since the payoffs of both players are already established. So we either have W2(k) or W1(k) with Ann playing, or W1(k) with Beth playing, or the game is over. Obviously at the beginning of the first round only the first subgame is possible, and at the beginning of the second round only the first three. Now each of these four subgames leads into three subgames, depending on the value of the award drawn in that round. These up to 12 subgames in each round have one or several Nash equilibria, and the analysis of the subgames of a given round depends on the Nash equilibria of the subgames in the round right after that round. Therefore the game has to be analyzed starting with the subgames of the last round, then proceeding with the subgames in the round right before that, and so on.

Recursive forms of the extensive forms of W2(r) and W1(r) are displayed below, where the W1(r-1) and W2(r-1) stand for the the corresponding r-1 subgames. Where an end vertex is labeled by "W2(r-1), W2(r-1)", this end vertex for the round should be replaces by the extensive form of the game W2(r-1), and where an end vertex is labeled by "W1(r-1), 2", for example, this end vertex is replaced by the extensive form of the game W1(r-1) for the corresponding player, where the other player has a fixed payoff (of 2, in the example).

3. Four Rounds.

In every case we get many subgame perfect Nash equilibria here, since in many situations more than one Nash equilibrium occurs---remember that we have a non zero-sum game!

The fourth round

As in the two-round variant, it is obvious how to play the last round, round 4 in this case: If you don't have an award yet, express interest!

Round 3

Note that the expected value of the award in each round is P(1)+2·P(2)+3·P(3).

Assume first the award available in round 3 is 1.

• If both express interest, then Ann gets the award of 1 with probability 1/2, and gets an expected value of P(1)+2·P(2)+3·P(3) in the fourth round with probability 1/2. Therefore the expected value for Ann in that case equals (1+P(1)+2·P(2)+3·P(3))/2. The same obviously holds for Beth.
• If Ann expresses interest, but Beth not, then Ann gets a value of 1 and Beth expects P(1)+2·P(2)+3·P(3) in round 4.
• If both don't express interest, then the probability of getting the award of expected value P(1)+2·P(2)+3·P(3) in round 4 is only 1/2, otherwise the player gets nothing, therefore the expected values for both players are (P(1)+2·P(2)+3·P(3))/2 in that situation.

This may show how we could attack the general case, with arbitrary P(1), P(2), and P(3), but also that this general analysis becomes rather complicated soon. Therefore, to simplify matters, let's from now on choose special probabilities P(1)=1/2, P(2)=1/3, P(3)=1/6. We get P(1)+2·P(2)+3·P(3)=5/3, and therefore

	interest	none
interest	4/3, 4/3	1, 5/3
none	5/3, 1	5/6, 5/6

This situation has three Nash equilibria: The two equilibria of one of the players expressing interest and the other not, and one mixed Nash equilibria of both expressing interest randomly in 1/3 of the cases, and not expressing interest in 2/3 of the cases. In that case, both compete in 1/3 · 1/3 of the cases, Ann gets the award in round 3 and Beth in round 4 in 1/3 · 2/3 of the cases, Beth gets the award in round 3 and Ann in round 4 in 2/3 · 1/3 of the cases, and none gets the award in round 3 in 2/3 · 2/3 of the cases. Therefore the expected payoff for Ann equals 1/9 · 4/3 + 2/9 · 1 + 2/9 · 5/3 + 4/9 · 5/6 = 4/27 + 6/27 + 10/27 + 10/27 = 30/27 = 10/9 in that case, and the same for Beth.

In the other situations in round 3, if the award available is 2 or 3, and both players still without award, we get Nash equilibria of both expressing interest, with expected payoffs of 11/6 for both, respectively of 7/3 for both. If one player already has the award at this stage, the player still playing just compares the award available with the expected award value of 5/3 in the next round.

Round 2

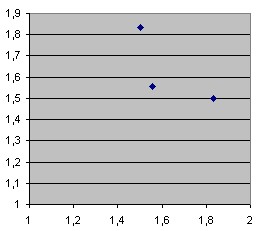
In round 2, we get three different scenarios, depending on which of the three Nash equilibria the players would choose in the round 3/award 1 case discussed above. In any one of the three scenarios, both players would not be interested in case of a value of 1, with expected payoffs of 1.5 versus 1.83 in the first scenario, of 1.83 versus 1.5 in the second one, and of 1.56 versus 1.56 in the third one. In case of a vlue of 2, there are three pure Nash equilibria in all three scenarios, namely both expressin interest, or just one of the players expressing interest, with uniform expected payoffs of 2 for both players in all three equilibria and all three scenarios. In the case of a vlue of 3, both players would express interest with expected payoffs of 2.5 for both. Again the cases where one of the players has already taken the award can be easily analyzed: The player still playing would just compare the value shown with the expected payoff of 2.

Round 1

If an award of value 1 is shown in round 1, nobody shows interest. The expected values for Ann and Beth are 1.83 and 2 in scenario 1, 2 and 1.83 in scenario 2, and 1.86 for both in scenario 3.

If an award of value 2 is shown in round 2, in any of the three scenarios describe above, we again get multiple Nash equilibria. Let's call these also scenarios: A in case Ann expresses interest and Beth not, B if Beth shows interest but not Ann, and C in case of a mixed Nash equilibrium. However, in scenarios 1 and 2 the mixed Nash equilibrium is Pareto dominated by one of the pure equilibria, therefore only in scenarion 3 scenarion C is really an option. The probabilities of the mixed strategies in this case are: Both show interest with probability 0.63.

If an award of value 3 is shown in round 1, both express interest. The expected values for Ann and beth are 2.58 in all three scenarios 1, 2, and 3.

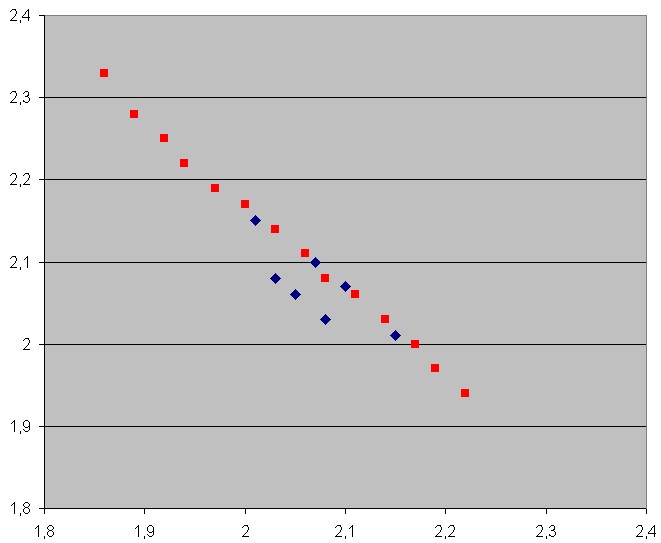Therefore we get 7 subgame perfect equilibria, scenarios 1A, 1B, 2A, 2B, 3A, 3B, 3C, depending which of the three Nash equilibria A, B, C the players would select in case of a 2 in round 1, and depending on which of the the three Nash equilibria 1, 2, 3 the players select in case of a 1 in round 3. The outcomes can be given in tabular form:

	A	B	C
1	2.01 , 2.15	2.07 , 2.1	not valid
2	2.1 , 2.07	2.15 , 2.01	not valid
3	2.03 , 2.08	2.08 , 2.03	2.05 , 2.05

The Broken Heart

Exercises

1. ...