Analysis of VNM POKER II

Prerequisites: All Theory Chapters, except maybe Chapter 9, and the first part on poker.

This chapter looks into two versions of VNM Poker---VNM POKER(2,r,m,n) and VNM POKER(4,4,3,5) in more detail, using mixed strategies. The first part is also an exercise how to work with parameters, and uses some algebraic manipulation of expressions, and some graphing of equations. The second part demonstrates the difficulties one faces when looking for mixed Nash equilibria in larger examples, and also that, although one player's Nash equilibrium mix draws against much more strategies than the other player's Nash equilibrium mix, playing such a mix may still be worthwhile in two-player zero-sum games.

• 1. VNM POKER(2,r,m,n)
  • 1.1 The case n/m ≥ (2r-1)/r
  • 1.2 Best Responses
  • 1.3 Reading the Opponent (optional)
  • 1.4 Mixed Nash equilibrium for n/m ≤ (2r-1)/r
  • 1.5 Small changes in the parameters
• 2. VNM POKER(4,4,3,5)
  • 2.1 Mixed Nash equilibria
  • 2.2 Suboptimal Strategies
• References
• Exercises and Projects

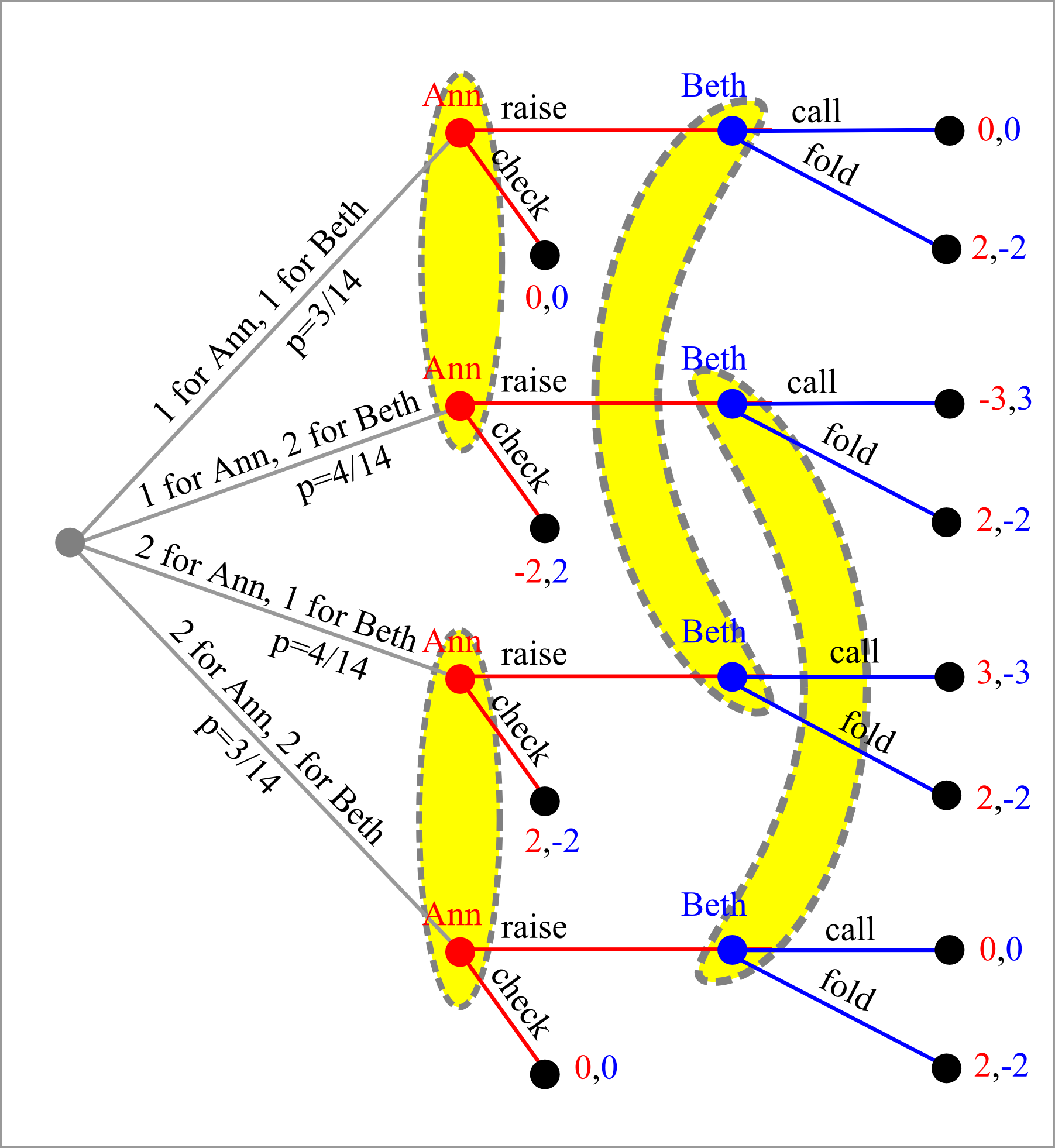
Recall from the first discussion of VNM Poker that we play with r cards of value 1 and r cards of value 2, with initial bet of m and a raised bet of n. We assume r ≥ 2, otherwise the game would have perfect information. The extensive form looks as follows.

In our case S=2, the pure strategies for Ann are the prudent CC (check in any case), the reasonable CR (check in case of a "1" and raises in case of a "2"), the silly looking RC (raise in case of a "1" and check in case of a "2") and the aggressive RR (raise in any case). Beth's pure strategies are the prudent FF (fold in any case), the reasonable FC (fold in case of a "1", call in case of a "2"), the counterintuitive CF (call in case of a "1", fold in case of a "2"), and the aggressive CC (call in any case). The normal form with the expectations for Ann (remember, it is zero-sum game) looks as follows:

These expressions are obtained as follows. For every fixed pair of strategies, let A_x,y be Ann's payoff provided both player stick to their chosen strategy and Ann gets a card of value x and Beth a card of value y. For instance, if Ann plays the aggressive RR and Beth plays the reasonable FC, then A_1,1=m , A_1,2=-n, A_2,1=m, and A_2,2=0. Then Ann's total expected payoff for the pair of chosen strategies equals

As noted in the first part, Ann's strategy CC is weakly dominated by strategy CR, and strategy RC is weakly dominated by RR, therefore both can be deleted. Similar, Beth's strategy FF is weakly dominated by FC, and her strategy CF is weakly dominated by CC. Thus the remaining normal form is

	FC	CC
CR	0	(n-m)r/(4r-2)
RR	((2r-1)m-rn)/(4r-2)	0

Note that the entry (n-m)r/(4r-2) is always positive. If the value ((2r-1)m-rn)/(4r-2) is not positive, then Ann's strategy CR weakly dominates RR, and Beth's strategy FC weakly dominates CC, therefore there is equilibrium in pure strategies CR versus FC with expected outcome 0 in that case.

The value ((2r-1)m-rn)/(4r-2) is non-positive if rn ≥ (2r-1)m, i.e. if n/m ≥ (2r-1)/r, i.e. if the increased bet n is considerably higher than the ante m. The values (2r-1)/r equal 3/2, 5/3, and 7/8 for r=2,3,4. Even for very large r, this value is always lower than 2. In particular, if raising means doubling, the analysis is already finished for every r. Then aggressive play, bluffing, will not occur, since it is too expensive.

Assume Beth plays FC in q of the cases, and CC in the remaining 1-q. Or in terms of behavior strategies, when holding a value of 1 Beth folds with probability q, and when holding a value of 2 Beth always calls. Ann's playoff when playing CR is (1-q)(n-m)r/(4r-2). This is larger or equal to Ann's payoff when playing CC, which is q((2r-1)m-rn)/(4r-2), if

In the same way we compute Beth's best response to Ann's mixed strategy of playing CR with probability p, and playing RR with probability 1-p (which again translates easily into the behavior strategy of checking with probability p when holding a value 1 card, and raising always with a card of value 2). When Beth plays FC, Beth's expected payoff equals -(1-p)((2r-1)m-rn)/(4r-2) and when she plays CC, Beth's expected payoff equals -p(n-m)r/(4r-2). After some calculations as above, we can see that both values are equal for p = ((2r-1)m-rn)/((r-1)m), let's call this value p^*. Moreover, Beth's payoff when she plays FC is smaller than her payoff when whe plays CC provided p < p^*. Beth should play CC when Ann plays CR with frequency less than p^*, when Ann plays too aggressively, bluffs too much. Conversely, Beth should play the lame FC when Ann plays CR more often than the value given above, that is, if Ann plays too lamely.

In essence, a clever Ann would complement the observed behavior of the opponent. Beth, on the other hand, should mirror the play she observes in Ann.

The key for effective play is to find out how the computer player plays by observing it playing repeatedly. Note also that it suffices to read the other player's behavior strategy, since any mixed strategy belonging to the same behavior strategy has the same payoffs. We also assume that Ann always raises and Beth always calls with a card of value 2---without that assumption the analysis would be much more difficult.

Of course, if players randomize, then we cannot tell the other's probabilities used after a few rounds, but after many rounds the Law of Large Numbers tells us that the frequencies observed are close to the probabilities used. The only problem is that we cannot observe all decisions---we don't see all of the other's decisions. If a player folds, then no player sees the others card, not even after the game is over.

What Beth can observe about Ann's play is how often Ann checks and raises, say 30% and 70% to give an example. We assume that Ann only checks with a card of value 1. Since on the long run, in about 50% of all rounds Ann has a "1", but only in 30% of all rounds Ann checks (with a "1"), in about 20% of all rounds, Ann must raise with a "1". Therefore in 20%/50% = 40% of the cases where Ann has a "1" she raises. In other words, Ann plays a mix of 60% CR and 40% RR.

Let us now discuss how Ann can observe Beth's strategy. We look only at the cases where Ann raises with a card of value 2. Let's say Beth calls in 70% of that cases, and when she calls she displays 39% of "1"s and 61% of "2"s. Among all these cases considered, Beth calls with a "1" with frequency 70%·39% ≈ 27%, Beth calls with a "2" with frequency 70%·61% ≈ 43%. These 43% are about 3/7, the fraction of considered cases where Beth holds a "2", given that Ann holds a "2", which confirms our assumption on Beth never folding with a "2". The only other option is to fold with a "1", which occurs in 30% of the cases considered. Therefore, when Beth has a "1" she calls in 27%/(27%+30%) ≈ 47% of the cases, Beth plays a mix of 53% FC and 47% CC in our example.

If n/m ≤ (2r-1)/r then there is no pure Nash equilibrium, therefore there must be a Nash equilibrium in mixed strategies, Ann playing CR with probability p, and RR with probability 1-p, and Beth playing FC with probability q, and CC with probability 1-q, with 0 < p < 1 and 0 < q < 1. Since each mix is a best response to each mix, and therefore each one of the two pure strategies is a best response to each mix, we conclude p = p^* = ((2r-1)m-rn)/((r-1)m)) and q = q^* = (n-m)r/((r-1)m) as discussed above.

Instead of in terms of n and m, both probabilities can also be expressed in terms of the ratio n/m:

The value of the game, Ann's payoff when both use these Nash equilibrium mixed strategies, equals

Of course this value of the game could also be computed as p^* · 0 +(1-p^*) · ((2r-1)m-rn))/(4r-2)) or as q^* · 0 + (1-q^*) · (n-m)r/(4r-2) or as q^* · ((2r-1)m-rn))/(4r-2)) + (1-q^*) · 0.

Note that this value is the product of the initial bet m and an expression in the ratio n/m and r. That means that, if we keep n/m and r fixed (and therefore change n proportional to m) the value is proportional to m. Or, the value per ante V/m only depends on r and the ratio n/m:

In order to answer the question of how the Nash equilibrium mixes would change if r is increased, or if n is increased, let us graph the values p^* and q^* also in terms of r and the ratio n/m. Remember that p^* and q^* are the percentages of Ann checking respectively Beth folding when holding a card of value 1. In these graphs the color indicates the value of p^* and q^*, purple being 0 (aggressive play), greenish being around 0.5, and red indicating 1. The contour curves are again combinations with constant p^* and q^*.

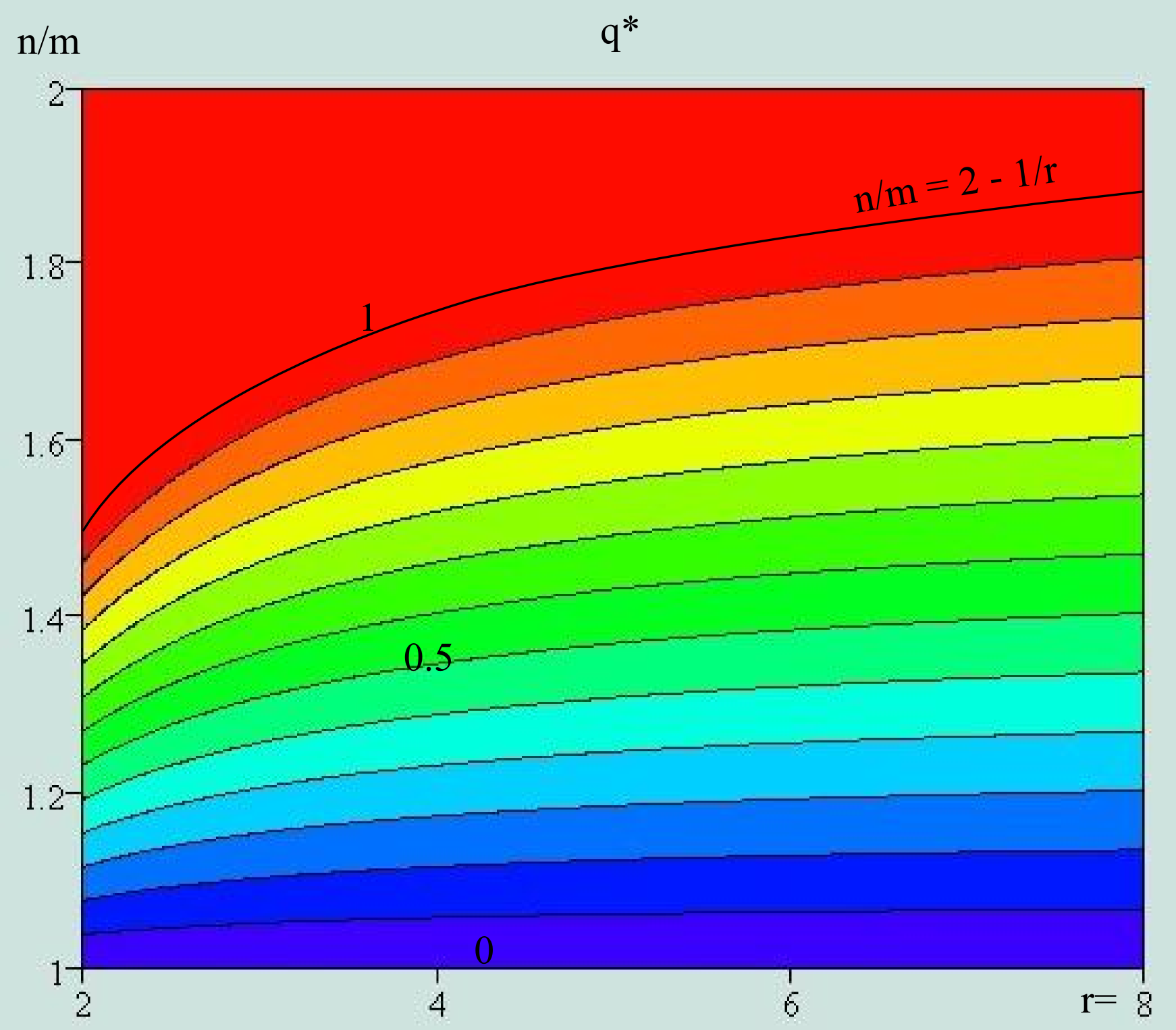
Again it can be easily seen that south of the curve n/m = 2 - 1/r, the mixes of Ann and Beth complement each other. Where Ann raises a lot with cards of value 1, Beth calls little, and vice versa. Just north of the curve Ann always checks with a "1", and Beth always folds with such a card. The stakes are too high for bluffing there.

From the graphs there follows that increasing r means that p^* increases slightly while q^* decreases. Increasing n slightly means a decrease of p^* and an increase of q^*. In any case, small changes of the parameters means small changes of p^* and q^*, except in the case if we cross the curve n/m = 2 - 1/r in which case p^* changes from 1 to 0 or conversely. Slight causes, but dramatic implications in that case.

	FFFF	FFFC	FFCF	FFCC	FCFF	FCFC	FCCF	FCCC	CFFF	CFFC	CFCF	CFCC	CCFF	CCFC	CCCF	CCCC
CCCC	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
CCCR	0.15	0.00	0.28	0.13	0.28	0.13	0.42	0.27	0.28	0.13	0.42	0.27	0.42	0.27	0.55	0.40
CCRC	0.55	0.02	0.40	-0.13	0.68	0.15	0.53	0.00	0.68	0.15	0.53	0.00	0.82	0.28	0.67	0.13
CCRR	0.70	0.02	0.68	0.00	0.97	0.28	0.95	0.27	0.97	0.28	0.95	0.27	1.23	0.55	1.22	0.53
CRCC	0.95	0.42	0.42	-0.12	0.80	0.27	0.27	-0.27	1.08	0.55	0.55	0.02	0.93	0.40	0.40	-0.13
CRCR	1.10	0.42	0.70	0.02	1.08	0.40	0.68	0.00	1.37	0.68	0.97	0.28	1.35	0.67	0.95	0.27
CRRC	1.50	0.43	0.82	-0.25	1.48	0.42	0.80	-0.27	1.77	0.70	1.08	0.02	1.75	0.68	1.07	0.00
CRRR	1.65	0.43	1.10	-0.12	1.77	0.55	1.22	0.00	2.05	0.83	1.50	0.28	2.17	0.95	1.62	0.40
RCCC	1.35	0.82	0.82	0.28	0.82	0.28	0.28	-0.25	1.20	0.67	0.67	0.13	0.67	0.13	0.13	-0.40
RCCR	1.50	0.82	1.10	0.42	1.10	0.42	0.70	0.02	1.48	0.80	1.08	0.40	1.08	0.40	0.68	0.00
RCRC	1.90	0.83	1.22	0.15	1.50	0.43	0.82	-0.25	1.88	0.82	1.20	0.13	1.48	0.42	0.80	-0.27
RCRR	2.05	0.83	1.50	0.28	1.78	0.57	1.23	0.02	2.17	0.95	1.62	0.40	1.90	0.68	1.35	0.13
RRCC	2.30	1.23	1.23	0.17	1.62	0.55	0.55	-0.52	2.28	1.22	1.22	0.15	1.60	0.53	0.53	-0.53
RRCR	2.45	1.23	1.52	0.30	1.90	0.68	0.97	-0.25	2.57	1.35	1.63	0.42	2.02	0.80	1.08	-0.13
RRRC	2.85	1.25	1.63	0.03	2.30	0.70	1.08	-0.52	2.97	1.37	1.75	0.15	2.42	0.82	1.20	-0.40
RRRR	3.00	1.25	1.92	0.17	2.58	0.83	1.50	-0.25	3.25	1.50	2.17	0.42	2.83	1.08	1.75	0.00

Obviously this example is more complex, and different to the case S=2 discussed above, an analysis of this family of games is no longer possible for general parameters r, m, and n, so we choose concrete values r=4, m=2, n=3. Even this concrete case is difficult enough to analyze.

Remember that pure strategies for Ann are four-letter words of "C"s and "R"s, and Beth's pure strategies are four-letter words of "F"s and "C"s. Moreover, after eliminating some weakly dominated strategies in the full normal form we got

Applying Brown's fictitious play, running say 1000 rounds in the Excel file BROWN10.xls, it is fairly convincing that Ann should choose 3/4 of strategy CCCR and 1/4 of RCCR. Beth's result is less clear, according to the results I obtained, Beth should mix about 5% of FFFC, about 37% of FFCC, and about 58% of FCCC. Fortunately, all we need to know is that Ann mixes only CCCR and RCCR in order to find the exact solution. Concentrating on these two of Ann's pure strategy, we get the following matrix:

Now let us use the graphical method for 2 × n zero-sum games. We draw four straight lines: The FFFC line from (0,0) to (1,49/60), the FFCC line from (0, 2/15) to (1,5/12), and so on. The height of the FFFC line at position x indicates Ann's payoff if Ann plays a mix of x of RCCR and 1-x of CCCR, and if Beth plays FFFC, and similar for the other three lines. Since Beth wants to maximize her own payoff, and therefore wants to minimize Ann's payoff, for each such x Beth would respond by the pure strategy that has the lowest height for this x-value. According to the graph, for 0 ≤ x ≤ 1/4 (a lot of CCCR), Beth would play FFFC, for 1/4 ≤ x ≤ 0.89, Beth would play FCCC, and otherwise CCCC. The curve on the top of the gray area indicates the payoff Ann can achieve when playing a mix of x of RCCR and 1-x of CCCR. Since Ann wants to maximize her payoff, she chooses that x where this curve has the largest height, so she chooses x=1/4. The expected payoff for Ann is 49/240 ≈ 0.2.

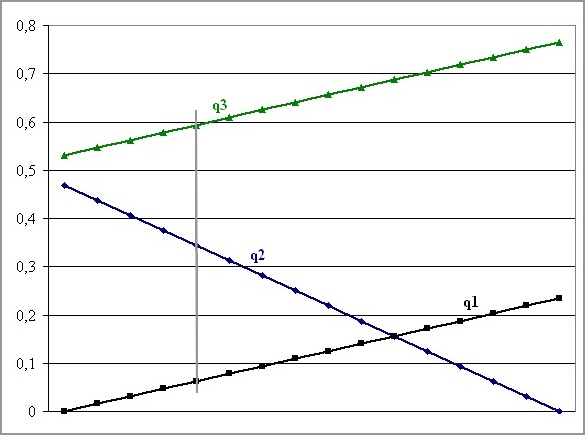
Note that it is a little odd, a coincidence, that three straight lines meet there, FFFC, FFCC, and FCCC. That means that Beth would mix these three strategies. To find the possible percentages q₁, q₂, q₃=1-q₁-q₂, we need again the Indifference Theorem and a little Algebra.

We know that both CCCR and RCCR are Ann's best responses to Beth's mix of q₁ of FFFC, q₂ of FFCC, and 1-q₁-q₂ of FCCC. Ann's payoff in both cases are on the left and the right of the following equation:

Playing a Nash equilibrium strategy in a zero-sum game guarantees a certain expected payoff, the value of the game, against any one of the other player's strategies. But the sad part is that this Nash equilibrium will not have a higher expectation against many other strategies of the other player, which are different to the Nash equilibrium counterpart. So, against sophisticated play, some less sophisticated play is not punished. In VNM POKER(2,r,m,n) for instance, all a player needs to know when playing against the Nash equilibrium is to avoid to fold or to check with the higher value card.

What about VNM POKER(4,4,3,5)?

Let us now look how pure strategies of Beth perform against Ann's optimal mix of 3/4 CCCR and 1/4 RCCR:

• FFFC, FFCC, FCFC, and FCCC are optimal against Ann's optimal mix. If Beth mixes these four pure strategies in any way, she will expect to lose only 49/240 ≈ 0.2
• CFFC, CFCC, CCFC, CCCC have an expectation of about -0.3 for Beth, when played against Ann's optimal mix.
• FFFF, FFCF, FCFF, FCCF have an expectation of about -0.49 against Ann's optimal mix.
• CFFF, CFCF, CCFF, and CCCF are Beth's weakest pure strategies, since they yield an expectation of about -0.58 for Beth.

............ and how Ann's pure strategies perform against the optimal mix of Beth using only "FFCC" and "FCCC":

• CCCR and RCCR are Ann's pure strategies where Ann achieves the optimal expectation of 49/240 ≈ 0.2 against Beth's mix mentioned above.
• The two strategies CCRR and RCRR are only slightly worse, giving an expectation of about 0.14.
• Ann's eight pure strategies CRCR, RRCR, CCCC, RCCC, CRRR, RRRR, CCRC, and RCRC yield an expected payoff for Ann between 0.01 and -0.06, when playing against Beth's mix mentioned.
• CRCC and RRCC are rather bad for Ann, giving an expectation of about -0.2,
• But the worst pure strategies for Ann are CRRC and RRRC, which yield an expectation of -0.26 for Ann, again when played against Beth's mix mentioned.

From these results, there follows, as usual, that if Ann plays the optimal mix mentioned, she will not gain an additional advantage if Beth plays andy mix of the four pure strategies FFFC, FFCC, FCFC, and FCCC. This translates into a behavior strategy of "F??C". You always fold with a lowest value, and always call with a highest value, but otherwise you can do whatever you want. On the other hand, every mixed strategy that sometimes calls with a lowest value and sometimes folds with a highest value will perform suboptimally against Ann's optimal mix.

On the other hand, a Beth playing the optimal mix will not gain an advantage against an Ann using any mix between CCCR and RCCR. Such a mix translates into the behavior strategy "?CCR" of always checking with a value of 2 or 3, always raising with a highest value of 4, but doing whatever with a lowest value of 1. However, every mixed strategy that sometimes raises with a value of 2 or 3, or sometimes checks with a velue of 4, will perform suboptimally against Beth's optimal mix of FFCC and FCCC.

• John von Neumann, Oskar Morgenstern, Theory of games and economic behavior, Princeton University Press 1953, 330.182 V89
• Gambit ...

Exercises

1. Assume you are playing many rounds of VNM POKER(2,r,m,n) as Beth against a first moving opponent Ann who assumes that you always call with a card of value 2, and who tries to estimate your ratio of FC versus CC as described above, and then play the best response. You certainly can mislead Ann by occasionally folding with a card of value 2, but the real question is whether such play could increase your expected value. Find out.