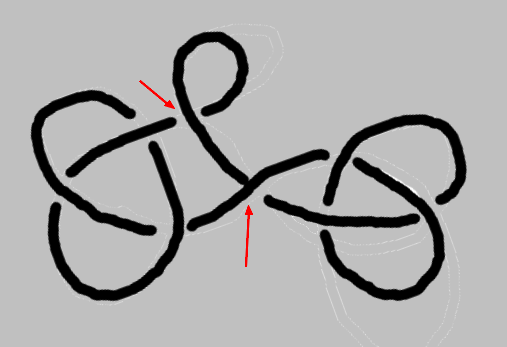Knots and Links

What they are

A knot is a closed curve embedded into 3-dimensional space. usually closed strings are used as models for knots. Note that different parts of the knot could be as close as we want, but they should not touch each other. An object being constructed of several knots, maybe linked together but not touching each other, is a link. If we take a part of such a string of a knot or link and move it, our perception is that we didn't change the knot or link. However, we would fundamentally change the knot or link if we would cut it open, move other parts through the gap, and close it again---therefore such an operation is not allowed when handling these objects. Two knots or links are equivalent (or simply "equal") if one can be deformed into the other without self-intersection.

An example of a knot and of a link are shown on the right. Usually knots or links are communicated in this graphical way. They are called projections.

A bug crawling on a knot would, on a foggy day, not be able to distinguish two different knots by crawling around. For such a bug, a knot would just be a closed curve. What distinguishes two different knots is not their shape itself but rather the embedding of them into 3-dimensional space.

Projections

Knots or links are visualized by means of projections. A crossing point is a point where more than one part of the curve projects to--- actually we can always avoid projections where three or more curves project to the same point, thus we can clarify these situations by depicting overcrossing and undercrossing. Strands are parts of the curves (in a given projection) between undercrossing and undercrossing, and regions are the different areas enclosed by the strands.

It is important to understand that the same knot or link could have several different projections, all looking different and having different numbers of crossing points. So, most values we observe in projections (like number of crossing points) are not relevant for distinguishing knots. There are however, as we will see, some few values attached to projections which are the same for any projection of the same knot. These values are called invariants. It is important to understand that if the value of an invariant is equal for two knots, it does not tell us anything, wheras if the values differ, the two knots must be different as well.

Look at a sequence of projections of the same knot.

Reidemeister Moves

1a		1b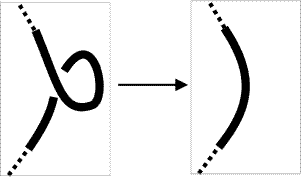
2a		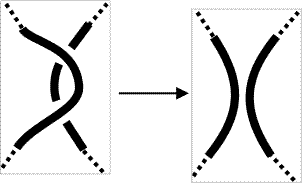2b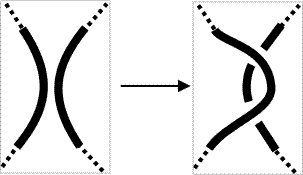
3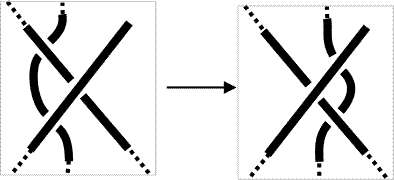

3-colorability of knots

A projection of a knot is called non-monochromatic 3-colorable or simply 3-colorable if the strands of the projection can be colored with three colors such that at every crossing point either one or all three colors are used, and for the total knot more than one color is used. See the example to the right. Move the mouse over the knot picture to color it, and click on the picture to decolor it.

Proof: It has to be shown that if we have a 3-coloring in a projection and make a Reidemeister move, then the resulting projection has also a 3-coloring. Actually, all strands in the focus window that have connections to the rest of the knot retain their color.

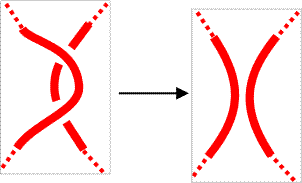
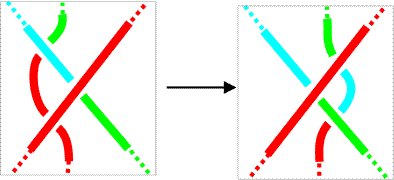
For Reidemeister move Ia, this is obvious. We just extend the color of the strand to both strands in the resulting projection.
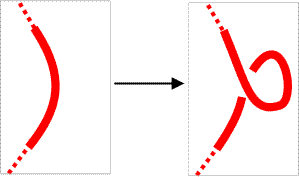For Reidemeister move 1b, the two strands in focus must have the same color, therefore we use that color for the resulting strand.

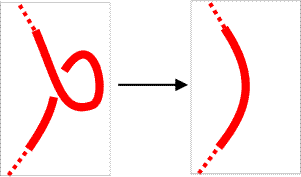
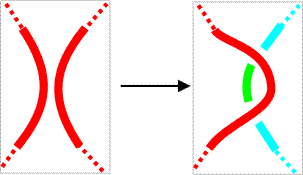
For Reidemeister move 2a, if the two strand have the same color, then we use this color for the new strand as well. If they have different colors, then the new strand gets the third color.
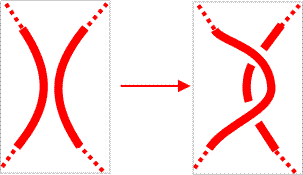
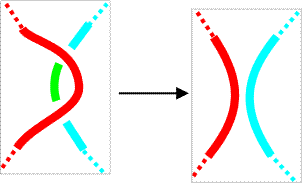
For Reidemeister move 2b, the right upper and lower strands must have the same color. This is the color of the resulting right strand.

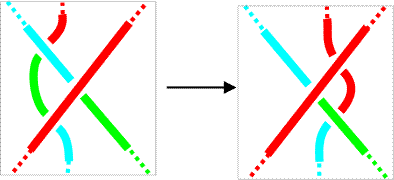
Finally, in Reidemeister 3 moves, all new strands with connections to the rest of the knot get the color the corresponding strand had. The short strand popping up in the middle can always be colored properly.

Consequently, since the simple projection of the unknot can obviously not be 3-colored (there is only one strand!), the trefoild knots and the other knot colored above are knotted (see Tietze's result of 1908). Moreover, since it is fairly easy to show that the figure-8 knot can not be 3-colored, the trefoil and the figure-8 are different.

How do we show that a knot is not 3-colorable? We assume it can. We start with one strand. It must have some color, say red.
Case 1: Assume that the uppermost crossing point sees only one color. Crossing points that see two strands with the same color must have all three with the same color, therefore we obtain this coloring , but this is monochromatic.
Case 2: Otherwise, all three colors occur at the uppermost crossing point . The middle crossing point sees different colors (red and green), thus it must see also blue, therefore the third strand must be blue. . But then the yet uncolored strand would have to have all three colors, blue, red, green, at the same time, a contradiction.

There is a fundamental difference between showing that a knot can not be 3-colored, and showing that a knot can not be transformed into the unknot. The first may be tedious, but it is a procedure whose time can be estimated in advance (in the worst case, if we have n strands, we just check all possible 3ⁿ possible assignments of colors to the strands and check whether some obeys the conditions). On the other hand, for the unknot problem we don't have an estimate, and we wouldn't know when to stop trying.

k-colorability of knots

With the notion of "3-colorability" we can only distinguish between those that can be and those that can not. To be able to classify knots further (into more than just two classes), we need more such notions. A projection of a knot is called nonmonochromatic k-colorable or simply k-colorable (for any natural number k>= 3) if the strands of the projection can be labeled with the numbers 0,1, ... k-1 such that at every crossing point twice the label x of the overcrossing equals the sume of the labels y and z of the undercrossing modulo k, (x ≡ y+z mod k) and if at least two labels are used. Note that a = b mod k if a and b differ by a multiple of k (or are equal).

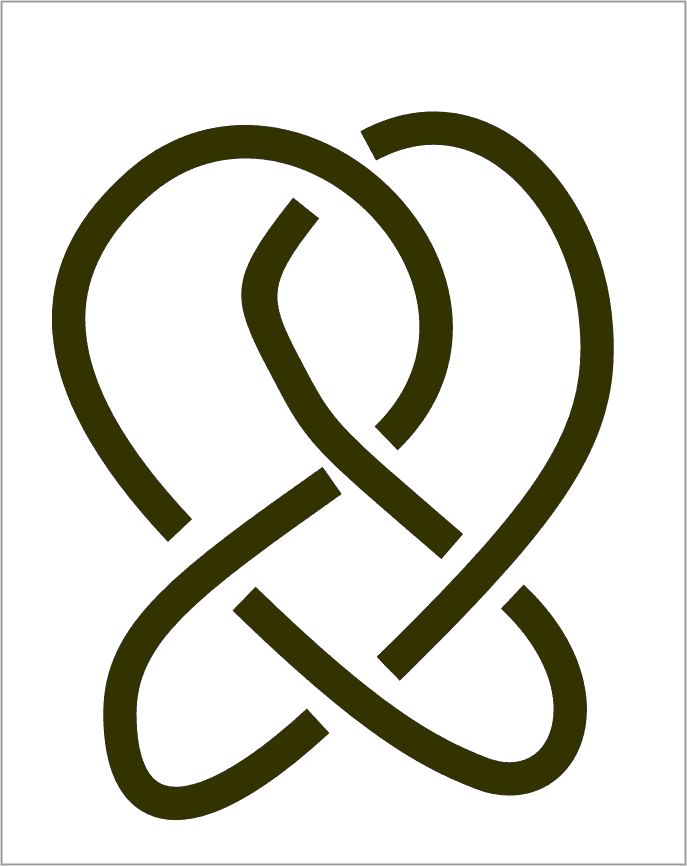
Note that we now have two different definitions for 3-colorability, one using really colors, and the other using the numbers 0, 1, 2 as labels. Ho0wever, both definitions are equivalent, since if 2 · x ≡ y + z (mod 3), with x, y, z the numbers 0, 1, 2, then either all three numbers x, y, z are identical or all three numbers x, y, z are different.

Moreover, we can even choose one of the strands to have the label 0 if the knot is k-colorable. The reason is that if we shift all labels by 1 mod k, (of course, shifting thereby k-1 to 0) then the resulting new labels also obey the k-colorability condition. Therefore,, if we want to check whether a given knot is k-colorable, we can just start by picking any strand and labeling it by 0. Then we choose another strand, having some common crossing point with the other one, and try to label it by 0, or by 1, or by 2, and so on until k-1. All other labels will follow in each case, and we either get contradictions for all these trials, or we find a k-coloring.

Alternating Projections

A projection is called alternating if undercrossings and overcrossings alternate when we move along the knot. Almost all projections on this page are alternating. Alternating projections are almost magic, as has been shown recently (23 years ago is very recent for mathematics):

The word reduced says that the projection should not have a simple twist, also called isthmus. The projections below is alternating, but not reduced. The isthmuses are indicated by arrows.