................
A knot is a closed curve embedded into
3-dimensional space. usually closed strings are used as models for knots.
Note that different parts of the knot could be as close as we want,
but they should not touch each other.
An object being constructed of several knots, maybe linked together but not touching each other,
is a link. If we take a part of such a string of a knot or link and move it,
our perception is that we didn't change the knot or link. However, we would fundamentally change
the knot or link if we would cut it open, move other parts through the gap, and close it again---therefore
such an operation is not allowed when handling these objects.
Two knots or links are equivalent (or simply "equal") if one
can be deformed into the other without self-intersection.
An example of a knot and of a link are shown on the right. Usually knots or links are communicated in this graphical way. They are called projections.
A bug crawling on a knot would, on a foggy day, not be able to distinguish two different knots by crawling around. For such a bug, a knot would just be a closed curve. What distinguishes two different knots is not their shape itself but rather the embedding of them into 3-dimensional space.
Knots or links are visualized by means of projections. A crossing point is a point where more than one part of the curve projects to--- actually we can always avoid projections where three or more curves project to the same point, thus we can clarify these situations by depicting overcrossing and undercrossing. Strands are parts of the curves (in a given projection) between undercrossing and undercrossing, and regions are the different areas enclosed by the strands.
It is important to understand that the same knot or link could have several different projections, all looking different and having different numbers of crossing points. So, most values we observe in projections (like number of crossing points) are not relevant for distinguishing knots. There are however, as we will see, some few values attached to projections which are the same for any projection of the same knot. These values are called invariants. It is important to understand that if the value of an invariant is equal for two knots, it does not tell us anything, wheras if the values differ, the two knots must be different as well.
Look at a sequence of projections of the same knot.
Also the question of when did people start looking into knots and links was raised in class. The answer is long time ago; even Phrygian people in the 4th century BC looked into knots, but it has not been mathematically considered until the end of the 19th century. Maybe knots seemed too complicated to solve.
Professor Prisner also talked about the pioneer of knot theory Kurt Reidemeister(1893-1971). He proved that all knot deformation can be reduced to three types of “moves” called the Twist Move (1a or 1b), Poke Move (2a or 2b) and a Slide Move (3), or all known as “Reidemeister Moves”.
| 1a |  |
1b |  |
| 2a |  |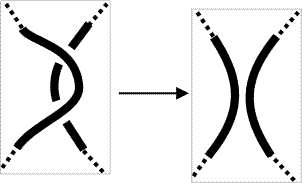
2b |  |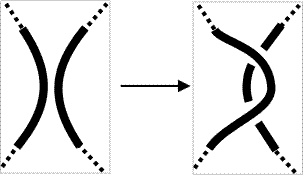
| 3 |  |
We also learned about knot or ink "invariants“, which is any property of the projection such that all projection of the same knot have the property or none has it. They are used to distinguish knots or links. But beware, just because two projections have same property, they are NOT necessarily identical!
Which of the following links are different, which are identical?
1) 
|
2)
|
3) 
|
4) 
|
5) 
|
6) 
|
From a link one gets an oriented link by orienting every component in one of the two possible ways. The linking number lk(L) of an oriented 2-component link is the sum of the values for crossing numbers between different components, +1 for right handed crossings, and -1 for left-handed crossings. Click on the pictures above to get an orientation and the corresponding sign.
Of course, we have many ways to orient a 2-component link, but the absolute value of the linking number |lk| remains the same. Why? Reversing the orientation of one component reverses all numbers.
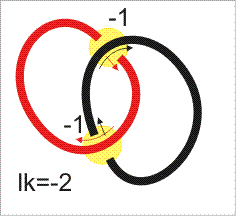
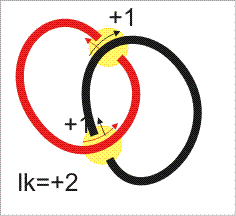
Therefore the links number 4 and 5 shown are different, and both are different from links number 1, 2 or 3. Actually links 1 and 2 are equivalent (the 2-component unlink) but different from number 3, the "Whitehead link", but this requires finer investigation. And links 5 and 6 are different, since the black part is knotted in number 6.
At the end of class, the definition of being non-monochromatic 3-colorable was stated, and it was shown that the usual projection of the trefoil knot has this property, wheras the usual projection of the unknot doesn't have it.