Braids

To produce a (3-)braid we need 3 strings of chords, one left, one in the middle, and one to the right. Then these strings move downwards, thereby changing positions repeatedly.

Let us first spend some time thinking about how braids could be communicated over the phone. When moving along a braid, we see that there are very few positions where the different strings change place. In the example to the right, these positions are indicated by a black line . Everywhere between, the left string remains left, the middle remains in the middle, and the right one remains right, indicated by the symbol "1".
"1"=
We can always avoid the situation where all three chords change position at the same time by tearing, pulling, and turining the strings a little. Then at these positions where change happens, either right strand and middle string change position,
"A"= , "A'"=
or the left stand and the middle string change position.
"B"=, "B'"=
And in each case, they can change position in two ways, as has been shown above. Therefore we can describe every 3-braid by a sequence of the letters "A", "A'", "B", "B'", and "1". For example, the the braid to the right is encoded as AB'B'B'ABAAB'AB'B'AB'AB'. Of course, the symbol 1 could also be added everywhere, so AB'1B'B'1ABA11AB'1AB'B'1A11B'A1B'11 does also encode the braid.

However, what is the "essence" of a braid. If one takes a braid, leaves top and bottom fixed, but changes the placement of the strings between without cutting any of them, the resulting is obviously supposed to be the "same" braid. But two different representations of the same braid may have different descriptions. For example, obviously the braids "AA'B" can be transformed into the braid "1B1". So both are different representations of the same braid. Or, the braid ABA equals the braid BAB.
It turns out that any two representations of the same braid cen be transformed into each other by repeatedly applying a few simple transformations:
AA'B
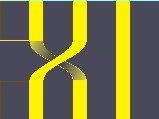1B1

ABA
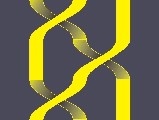BAB
Theorem: Two encodings, strings of the five symbols "A", "A'", "B", "B'", and "1", represent the same braid provided one can be transformed into the other by repeatedly

In this applet you can create braids by putting the five ingredients "A", "A'", "B", "B'", and "1" together. But you can also change representations by deleting "1"s, or replacing "AA'" or "BB'" or "A'A" or "B'B" parts by "1", or interchanging "ABA" and "BAB", respectively "B'A'B'" and "A'B'A'".

Although that, starting with a long encoding, reducing it using the laws above is relatively easy, it is not at all easy to decide whether two given encodings represent the same braid. The reason for that is that in order to transfrom one encoding into another one, in most cases we have to lengthen the encoding first, and only after some time would reduce the length to obtain the other encoding. Take the following example:
BAABA' = BAABA'B'B = BAABA'B'A'ABAA' = BAABA'B'A'BABA' = BAB'BABA'B'A'BABA' = BAB'BABB'A'B'BABA' = BAB'ABAB'A'B'BABA' = BAB'ABAB'A'ABA' = BAB'ABAB'BA' = BAB'ABAA' = BAB'AB