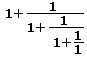
4b: Compute the value of the following compound fraction:

1: Explain the Pigeonhole principle
| 79% |
2a:
Assume 1200 people are in the same room. How many people can you guaranteed find
that celebrate their birthday on the same day?
2b:
Assume 1500 people are in the same room. How many people can you guaranteed find
that celebrate their birthday on the same day?
| 73% |
3a: List the first ten Fibonacci numbers
| 100% |
3b: What has the Golden ratio to do with Fibonacci numbers?
| 75% |
4a:
Compute the value of the following compound fraction:
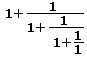
4b:
Compute the value of the following compound fraction:

| 63% |
5a:
Write the number 60 as a sum of distinct nonconsecutive Fibonacci numbers.
5b:
Write the number 70 as a sum of distinct nonconsecutive Fibonacci numbers.
| 90% |
6a:
Write the number 130 as a product of prime numbers.
6b:
Write the number 126 as a product of prime numbers.
| 67% |
7a: Who gave the first proof that there are infinitely many prime numbers?.
| 0% |
7b: How many prime numbers are there?.
| 83% |
8: Is the number 123 + 12311 prime? Why or why not?
| 18% |
9a:
Reduce 3·5·7·11·13+1 modulo 11.
(Meaning, find that number among 0,1,2,...10 that is equivalent to
3·5·7·11·13+1 (mod 11).)
9b:
Reduce 3·5·7·11·13+1 modulo 7.
(Meaning, find that number among 0,1,2,...6 that is equivalent to
3·5·7·11·13+1 (mod 7).)
| 38% |
10a:
It is Monday today. What day will there be in 789 days?
10b:
It is Monday today. What day will there be in 779 days?
| 50% |
11: When are two numbers "equivalent modulo 11"?
| 30% |
12: What does the Art Gallery Theorem say?
| 40% |
| 13a: Find a 3-coloring of the vertices (such that every triangle has all three colors) of the following triangulation of an art gallery. |
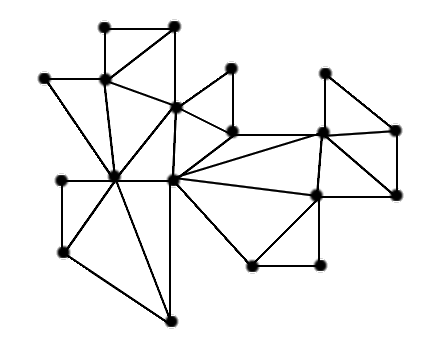 |
| 13b: Find a 3-coloring of the vertices (such that every triangle has all three colors) of the following triangulation of an art gallery. |
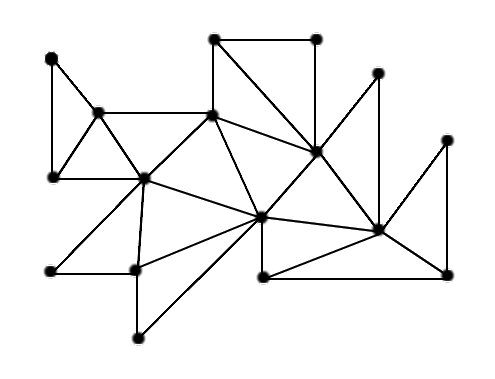 |
| 88% |
14: Explain a simple procedure how to produce another golden rectangle of different size from a given golden rectangle.
| 75% |
15a:
How many edges does a convex polyhedron with 20 vertices and 11 faces have?
15b:
How many edges does a convex polyhedron with 15 vertices and 18 faces have?
| 69% |
16a:
You have a polyhedron with 14 faces, all of them triangles. How many edges does the polyhedron have?
16b:
You have a polyhedron with 16 faces, all of them triangles. How many edges does the polyhedron have?
| 46% |
17a:
Which one of the following three graphs is a plane graph?
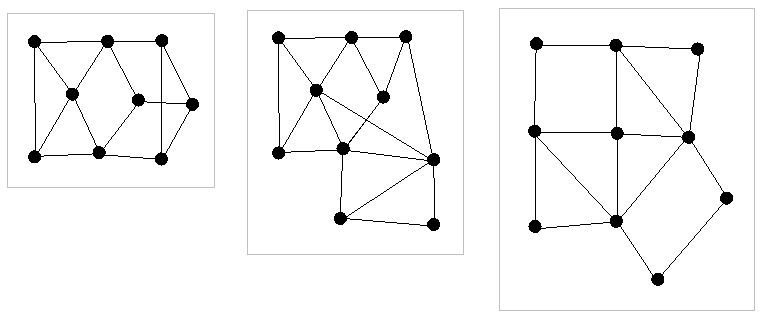
17b:
Which one of the following three graphs is a plane graph?
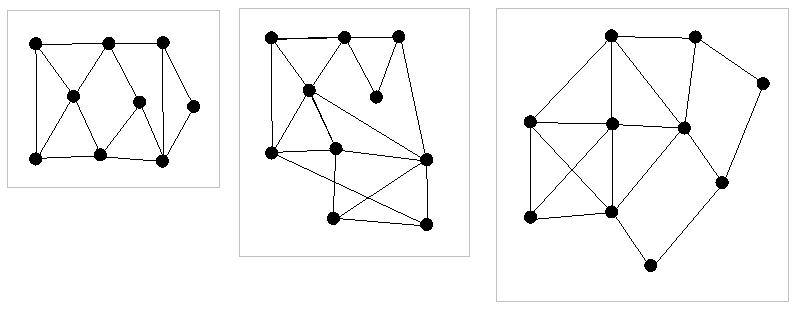
| 79% |
18: For the plane graph in the previous question, draw its dual.
| 54% |
19: Explain what Euler's polyhedron formula states about polyhedra. Who proved this result?
| 45% |
 20:
Does the graph to the right have an open or closed Eulerian tour?
If it doesn't, why not, if it has, write it down (as a sequence of the vertices).
20:
Does the graph to the right have an open or closed Eulerian tour?
If it doesn't, why not, if it has, write it down (as a sequence of the vertices).
| 35% |